カノニカル分布におけるエネルギーのゆらぎの計算

この記事ではカノニカル分布におけるエネルギーのゆらぎの計算方法と，その評価から実際にエネルギーのゆらぎが殆どないことを紹介します。

あわせて読みたい

カノニカル分布における理想気体の分配関数の計算（古典近似） カノニカル分布の理想気体について古典近似の分配関数の計算方法を紹介し，この分配関数を用いて様々な物理量を導出します。

カノニカル分布とは

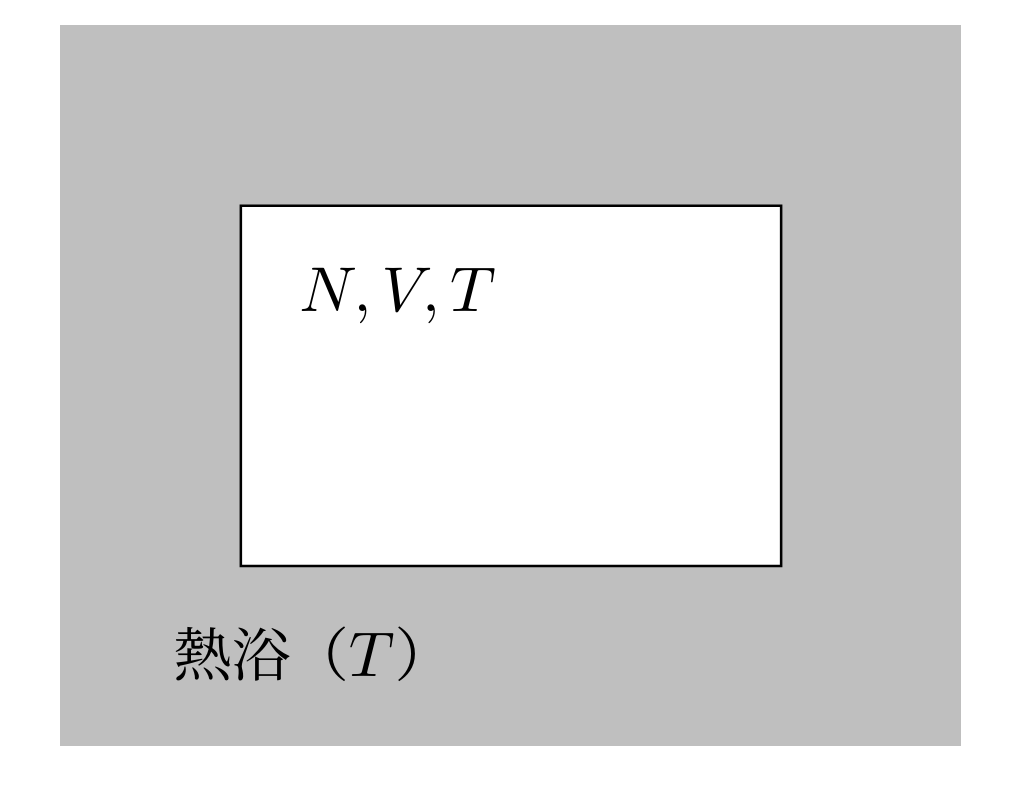
通常，カノニカル分布とは，粒子数 \(N\)，体積 \(V\)，温度 \(T\) が一定であるという条件の系が従う分布のことを指します。

また，このカノニカル分布で重要な値として次で与えられる分配関数というものがあります。\[Z_C=\sum_{n=1}^{\infty} e^{-\beta E_n}\]

上の分配関数は量子近似におけるものであり，古典近似での分配関数は \(\sum\) を \(\int\) に置き換え，位相空間で積分した \[Z_C=\frac{1}{h^f} \int \cdots \int e^{-\beta E} dp_1 \cdots dp_f dq_1 \cdots dq_f \] が使われます

カノニカル分布の分配関数の導出については次の記事で扱っているのでご覧ください。

あわせて読みたい

【量子統計力学】カノニカル分布の特徴と分配関数の導出 ミクロカノニカル分布とカノニカル分布の違いや，カノニカル分布における分配関数の求め方についてわかりやすく紹介します。

エネルギーのゆらぎの計算

カノニカル分布とは前述の通り，熱浴に接することで温度を固定させたものであり，エネルギーを固定させたものではありません。

つまり，この系でエネルギー \(E\) はある程度幅がある訳ですね。

ここで，実際にエネルギーはどの程度ばらつきがあるものなのかを考えてみます（このばらつきをエネルギーのゆらぎといいます）。

ゆらぎを調べるためには

を計算すれば評価することが出来そうです。ということで，以下ではエネルギーの平均値を調べましょう。

あわせて読みたい

カノニカル分布のエントロピーやエネルギー，その他物理量の導出方法 カノニカル分布におけるエントロピー S や自由エネルギー F を分配関数を用いて導出する方法を紹介します。

分散の計算

エネルギーの平均値は分配関数 \(Z_C\) を用いて \[\overline{E}=\sum_{n=1}^{\infty}\frac{E_n e^{-\beta E_n}}{Z_C}=\frac{1}{Z_C}\sum_{n=1}^{\infty} E_n e^{-\beta E_n}\] と書くことができたので，両辺に \(Z_C\) をかけ，分配関数の定義式を代入すると \[\overline{E}\sum_{n=1}^{\infty} e^{-\beta E_n}=\sum_{n=1}^{\infty} E_n e^{-\beta E_n}\] この式の両辺を \(\beta\) で微分します。すると合成関数の微分に注意して \[\frac{\partial \overline{E}}{\partial \beta}\sum_{n=1}^{\infty} e^{-\beta E_n}-\overline{E}\sum_{n=1}^{\infty} E_n e^{-\beta E_n}=-\sum_{n=1}^{\infty} E^2_n e^{-\beta E_n}\] 再び \(Z_C\) で割ると \[\frac{\partial \overline{E}}{\partial \beta}-\overline{E}^2 =-\overline{E^2}\] 従って

\[\overline{E^2}-\overline{E}^2=-\frac{\partial \overline{E}}{\partial \beta}\]

となり，エネルギーのゆらぎを示すことが出来ます。ここで，\(\beta\) を \(k_B,T\) を使って戻してあげると

\[\begin{align} \overline{E^2}-\overline{E}^2 &= -\frac{\partial \overline{E}}{\partial \beta}=k_B T^2 \left(\frac{\partial \overline{E}}{\partial T} \right) \\ &=k_B T^2 C_V\end{align}\]

と比熱 \(C_V\) を使って表すことが出来ます。

あわせて読みたい

定積モル比熱と定圧モル比熱の定義と他の物理量との対応 定積モル比熱と定圧モル比熱について，その定義と内部エネルギーやエントロピーとの対応を紹介します。

ゆらぎの評価

上の計算から更に平方をとって，標準偏差は \[\sqrt{\overline{E^2}-\overline{E}^2}=\sqrt{C_V k_B} T \] と求まりました。これから実際のゆらぎがどの程度になるかをランダウの記号 \(O(X)\) を使って考えてみます。

ランダウの記号 \(O(X)\) とは \(X\) 程度の値であることを示します。例えば \(2x^5+x\) は \(x\) が十分大きいとき \(x^5\) の程度に依存するので \[2x^5+x=O(x^5)\] と書くことが出来ます。

定積比熱 \(C_V\)，エネルギー平均値はともに \(C_V=O(N)\) ，\(\overline{E}=O(N)\) と評価すると，エネルギー平均値に対する標準偏差は

\[\frac{\sqrt{\overline{E^2}-\overline{E}^2}}{\overline{E}}=O \left( \frac{1}{\sqrt{N}} \right)\]

となります。これより，系を構成する粒子数が非常に多い場合，そのエネルギーの相対的な偏差は０に収束するため，平均値に近いものとして扱って良いことがわかります。