この記事ではカノニカル分布におけるエントロピー \(S\) や自由エネルギー \(F\) を導出する方法を紹介します。
カノニカル分布における分配関数
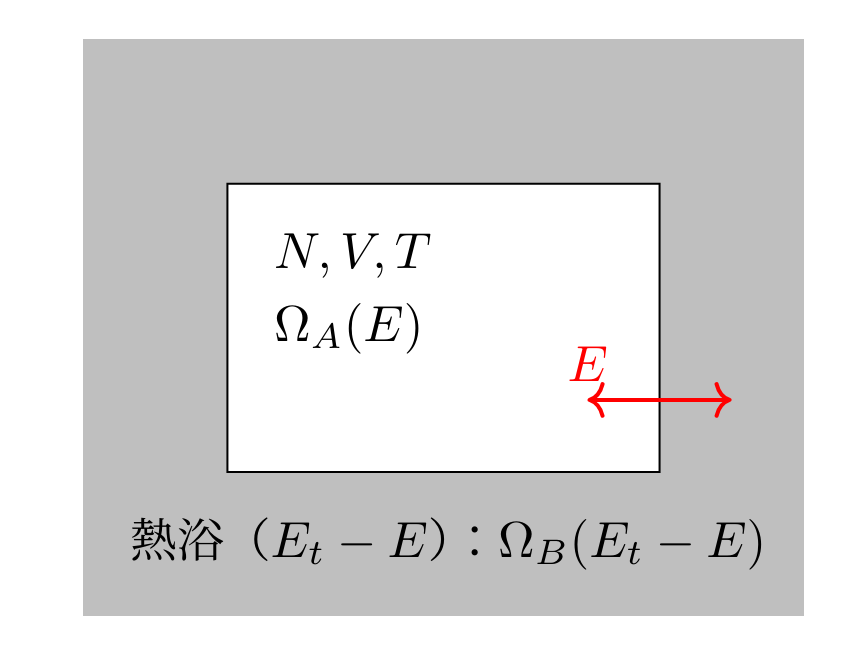
カノニカル分布における分配関数は \[Z_C=\sum_{n=1}^{\infty} e^{-\beta E_i}\] とかけて,これより \(E=E_i \; (i=1,2,\cdots)\) の実現する確率は \[P(E_i)=\frac{e^{-\beta E_i}}{Z_C}\] と表すことが出来たのでした。
分配関数の導出を知りたい方はこちら
以下ではこの条件をもとに,カノニカル分布における様々な物理量を計算してみましょう。以降,簡単のために \(P(E_n)\) を \(P_i\) と表記します。
カノニカル分布における物理量
量子論を適応したカノニカル分布では,ある物理量 \(A\) の平均は \[\langle A \rangle =\sum_{i=1}^{\infty} A_i P_i=\sum_{i=1}^{\infty} \frac{A_i }{Z_C}e^{-\beta E_i}\] を計算することで求めることが出来ます。分配関数を外に出してあげると \[
\langle A \rangle = \frac{1}{Z_C} \sum_{i=1}^{\infty} A_i e^{-\beta E_i}
\] となります。以下では \(A\) に様々な物理量をいれてその系における物理量の平均値を求めます。
エネルギーの計算方法
カノニカル分布のエネルギー \(E\) を計算します。 \(E\) を求める場合,\(A\) を \(E\) に書き換えて \[
\langle E \rangle =\frac{1}{Z_C}\sum_{i=1}^{\infty}E_i e^{-\beta E_i}\] とすれば良いですね。
 あんとら
あんとら統計力学では通常 \(\langle E \rangle=E\) とする表記が多いです
ここでもそれに倣い,以下では \(E\) と書き表します
ここで1つのテクニックではあるのですが, \(Z_C\) を \(\beta\) で微分したものを考えましょう。すると \[\frac{\partial Z_C}{\partial \beta}=\frac{\partial }{\partial \beta}\sum_{i=1}^{\infty} e^{-\beta E_i}=-\sum_{n=1}^{\infty}E_i e^{-\beta E_i}\] となり,求める \(E\) の値にかなり近い値が出てくることがわかります。よって
\[E=-\frac{1}{Z_C}\frac{\partial Z_C}{\partial \beta}=-\frac{\partial }{\partial \beta} \log Z_C\]
とすれば,これから\(E\) は分配関数 \(Z_C\) の微分だけで求められることがわかります。すごいですよね!これは統計力学においてはかなり重要な公式として扱われます。結果だけでも是非覚えておきましょう。
尚,\(\beta\) を使わずに \(E\) を表すと \[E=k_B T^2 \frac{\partial \log Z_C}{\partial T}\] と出来ます。
エントロピーの計算方法
カノニカル分布におけるエントロピー \(S\) も同様に求めます。
エントロピーの定義から直接計算すると \[\begin{align}
S&=-k_B \sum_{i=1}^{n}P_i \log P_i \\
&=-k_B \sum_{i=1}^{n} \frac{e^{-\beta E_i}}{Z_C} \log \frac{e^{-\beta E_i}}{Z_C} \\
&=-k_B \sum_{i=1}^{n} \frac{e^{-\beta E_i}}{Z_C}(-\beta E_i -\log Z_C) \\
&= \beta k_B \color{red}{\sum_{i=1}^{\infty}\frac{E_i e^{-\beta E_i}}{Z_C} } +k_B \log Z_C \color{blue}{\sum_{i=1}^{\infty} \frac{e^{-\beta E_i}}{Z_C}}
\end{align}\] ここで
- 赤字部分は上で求めた \(E\) そのものである
- \(\beta =1/k_B T\) である
- 青字部分は分配関数の定義から1になる
ことを使うと \(S\) は \[\begin{align}&S=\frac{E}{T}+k_B \log Z_C \\ &=k_B T \frac{\partial \log Z_C}{\partial T}+k_B \log Z_C \end{align}\] と計算することが出来ます。
ヘルムホルツの自由エネルギーの計算
ヘルムホルツの自由エネルギー \(F\) も計算します。熱力学関係式 \(F=E-TS\) より,\(S\) について解くと \[S=\frac{E}{T}-\frac{F}{T}\] です。ところで,先程の求めたエントロピー \(S\) は \[S=\frac{E}{T}+k_B \log Z_C \] であったのでこれを比較することでヘルムホルツの自由エネルギー \(F\) は
\[F=-k_B T \log Z_C\]
であることがわかります。これもまた統計力学ではよく使われます( $F$ が求まると他の物理量も求めやすい)。
他の物理量の計算
エネルギー \(E\),エントロピー \(S\),自由エネルギー \(F\) が求まることで,他の物理量も計算することが出来ます。
【圧力 \(p\) 】
熱力学関係式より \[p=-\left(\frac{\partial F}{\partial V} \right)_{N,T}=k_B T\left(\frac{\partial \log Z_C}{\partial V} \right)_{N,T}\]
【化学ポテンシャル \(\mu\) 】
熱力学関係式より \[\mu =\left(\frac{\partial F}{\partial N} \right)_{V,T}=-k_B T\left(\frac{\partial \log Z_C}{\partial N} \right)_{V,T}\]



以上の流れからわかる通り,カノニカル分布では分配関数を求めることさえ出来てしまえば,大半の物理量は少し計算するだけで求めることが出来てしまいます
これこそが,統計力学において分配関数が非常に重要であると云われる所以であるといえます




コメント