【量子統計力学】カノニカル分布の特徴と分配関数の導出

2024年4月16日2025年1月6日

この記事では量子論におけるカノニカル分布の特徴と分配関数 \[
Z_C=\sum_{i=1}^{\infty} e^{ -\beta E_i }\] の求め方をまとめます。

カノニカル分布とは

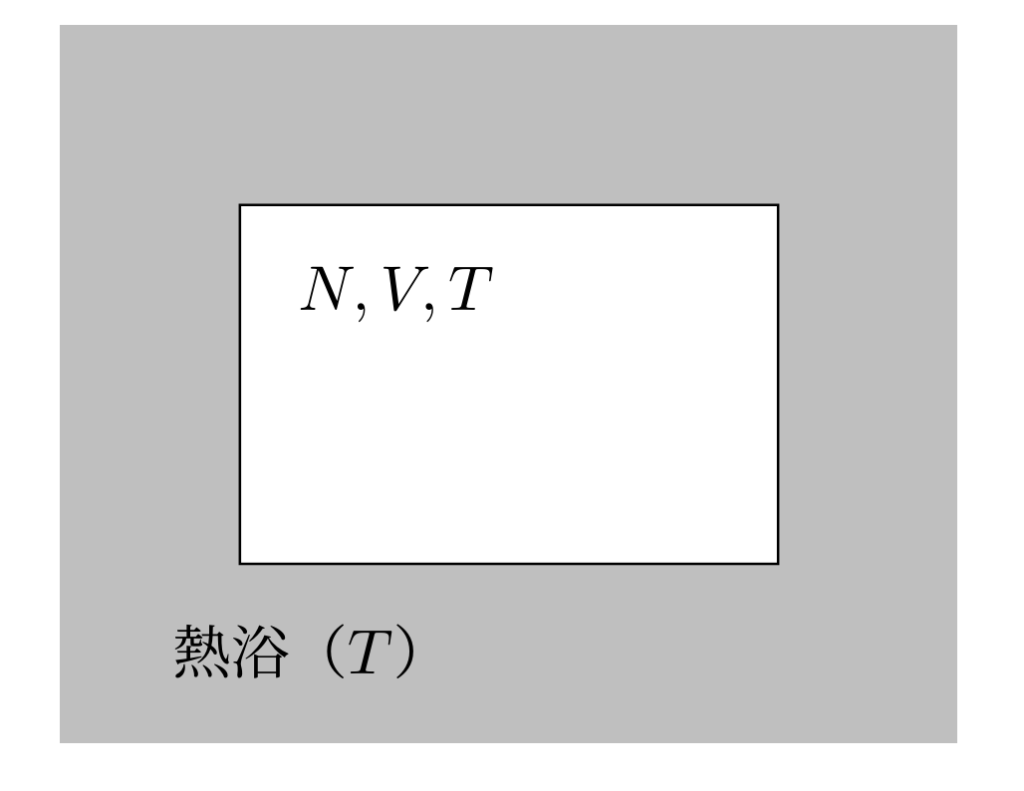
分配関数の導出に入る前にまずはカノニカル分布（正準集団）と呼ばれるものについて簡単に説明します。

通常，カノニカル分布とは粒子数 $N$，体積 $V$，温度 $T$ が一定であるという条件の系が従う分布のことを指します。

あんとら

図のような熱浴に接した系として考えることが多いです

同じような名称としてミクロカノニカル分布と呼ばれるものもありますが，ここで一度この二つについて何が違うのか比較しましょう。

二つの分布の違い

ミクロカノニカル分布	カノニカル分布
系は，粒子数 $N$，体積 $V$，エネルギー $E$ が一定	系は，粒子数 $N$，体積 $V$，温度 $T$ が一定

あんとら

エネルギーの変化が可能か否かというのがカノニカル分布とミクロカノニカル分布の大きな違いであるといえます

エネルギー $E$ を常に一定にしなくてはならないミクロカノニカル分布に比べ，温度 $T$ を一定にするだけで良いカノニカル分布は実験と相性が良く，様々なところで使われます。

分配関数の導出

統計力学での重要な目標として

様々な微視的な状態の中からある一つの状態が出現する確率を求める

というものがあります。分配関数を求めるにあたって，まずはこの目標に従いカノニカル分布での出現確率について考えましょう。

また，出現確率を計算する前に改めてカノニカル分布の系の設定を整理します。

カノニカル分布系の設定

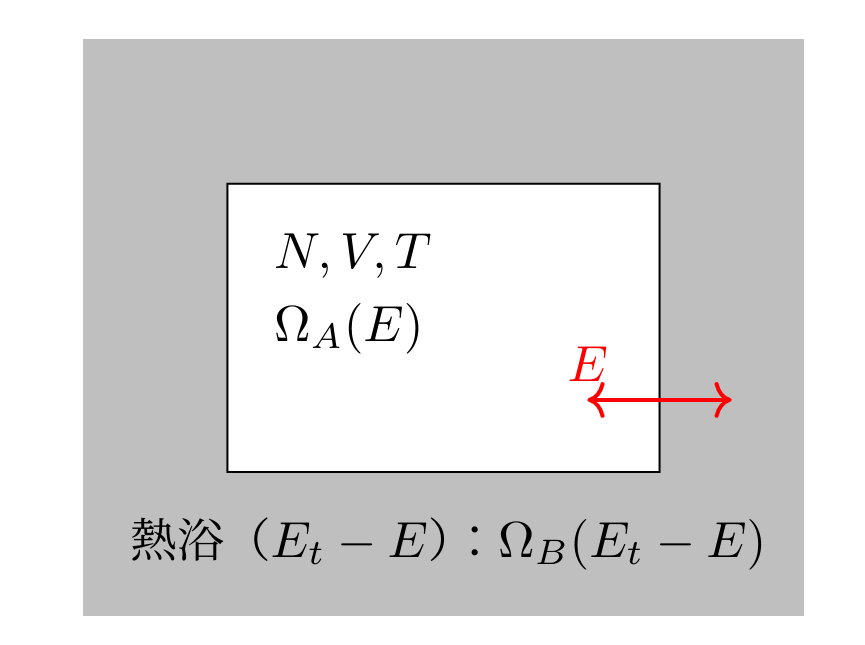
系を A とし，系を覆っている熱浴を B とする
A と B の合成系は孤立しており，A と B のエネルギー総和は $E_t$ で一定（ t は total の意）
A の粒子数を $N$，体積を $V$ とし，これらは常に一定
A のエネルギーは $E$ であるとする（$E$ は変数）
エネルギーが $E$ であるときの微視的状態の数を $\Omega (E)$ とする

設定がやや多くなりましたが，この設定のもとで，ある状態の出現する確率と分配関数を次の３つのステップに分けて導出します。

STEP１：状態の出現する確率を求める

まず，A のエネルギーが $E$ であるので，熱浴 B のエネルギーは $E_t -E$ と表すことが出来ます。

これより，あるエネルギー $E$ における微視的な状態の数は \[\Omega_A (E) \cdot \Omega_B (E_t -E) \] となります。¹

あんとら

エネルギーが $E$ のときにA の現象が状態ⅰ，状態ⅱ，…とあって，Bの現象が状態Ⅰ，状態Ⅱ，…とあるので，このときの合成系の場合の数は積の事象で表されます

このエネルギー変数 $E$ は $[0,E_t]$ を離散的に動きます。従って，全エネルギー $E_t$ 通りに対する現象の数 $\Omega_t (E_t)$ は $E$ について和をとれば良く \[\Omega_t (E_t) =\sum_{E} \Omega_A (E) \cdot \Omega_B (E_t -E)\] と書けます。これより，エネルギー $E$ の状態が出現する確率 $P(E)$ は \[P(E)=\frac{\Omega_A (E) \cdot \Omega_B (E_t -E) }{\Omega_t (E_t)}\] と表すことが出来ます。

STEP２：$\Omega_B$ をテイラー展開する

次に，$\Omega_B (E_t-E)$ の対数をとり，$E$ に関してテイラー展開します。すると \[\begin{align}\log \Omega_B (E_t-E) &= \Omega_B (E_t) -\left. \frac{\partial \log \Omega_B}{\partial E} \right|_{E=0}E \\ &=\Omega_B (E_t)-\frac{E}{k_B T} \end{align}\] よって \[\Omega_B (E_t-E)=\Omega_B (E_t) \exp \left( -\frac{E}{k_B T} \right)\] と表すことが出来ます。

対数を取って計算するとボルツマンの式 $S=k_B \log \Omega$ が使えるのであらかじめ対数をとっています。また， \[\frac{1}{T}=\frac{\partial S}{\partial E}\] に $S=k_B \log \Omega$ を代入して計算を進めています（勿論対数を取らずに計算することも出来ます）。

あんとら

$E_t$ は定数なので $\Omega_B$ を定数と指数関数の積にわけることが出来ました

STEP３：確率と分配関数の導出

STEP１，STEP２から確率 $P(E)$ を新たに書き直すと \[P(E)=\frac{\Omega_A (E) \cdot \Omega_B (E_t)}{\Omega_t (E_t)} \exp \left( -\frac{E}{k_B T} \right)\] と書き直すことが出来ます。ここで

$\Omega_B (E_t),\Omega_t (E_t)$ は定数
$\Omega_A (E)$ はエネルギーの縮退の数（指数部分に比べて遥かに影響が少ない）

であるので，結局，A がエネルギー $E_i$（$n=1,2,\cdots$）を取る確率は $e^{-E_i/k_B T}$ に比例することがわかります。

この $\displaystyle \exp \left( -\frac{E_n}{k_B T} \right)$ のことをボルツマン因子といいます。ここで逆温度と呼ばれる量 \[
\beta =\frac{1}{k_B T}
\] を導入するとこれはより簡単に $e^{-\beta E_i}$ と書くことが出来ます。

また，これより確率 $P(E_i)$ は定数を $C$ として \[P(E_n)=C e^{-\beta E_i}\] とおけます。この定数は規格化条件 \[\sum_{n=1}^{\infty} P(E_n)=C \sum_{n=1}^{\infty} e^{-\beta E_i}=1\] より

\[C=\frac{1}{\sum_{n=1}^{\infty} e^{-\beta E_i}}\]

と定まるので，この $\displaystyle \sum_{n=1}^{\infty}e^{-\beta E_i}$ を分配関数とすることで導出することが出来ます。

また，カノニカル分布の分配関数は通常 $Z_C$ と書かれることが多いので，ここでもその例に倣って $Z_C$ を使い，上の式の規格化定数 $C$ を書き直します。²

するとカノニカル分布である状態 $n$ をとる確率 $P(E_i)$ は

\[P(E_i)=\frac{e^{-\beta E_i}}{Z_C}\]

と表すことが出来るようになります。カノニカル分布ではこの分配関数をもとに様々な物理量を求めていきます。

分配関数を使って様々な物理量を導出する方法