無限に深い井戸型ポテンシャルの束縛問題をわかりやすく

量子力学の典型的な問題である「無限に深い井戸型ポテンシャル」問題について紹介します。

無限に深い井戸型ポテンシャル

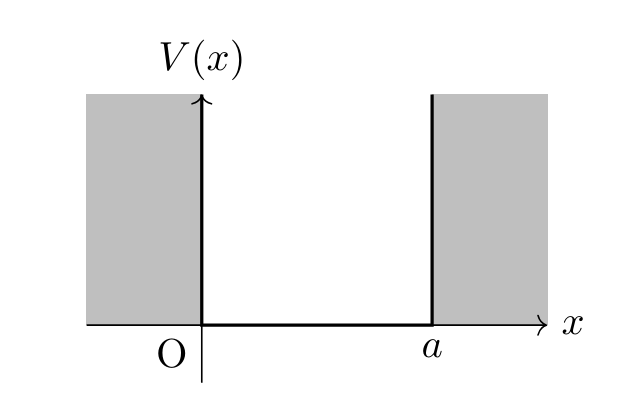
無限に深い井戸型ポテンシャルとは，次のような設定のもとで粒子がどのような振る舞いをするかについて調べる問題です。

ポテンシャルが無限に高い，すなわち \(V(x)= \infty\) のところでは粒子は２つの壁の外に出ることができない状態を考えます。この設定で時間依存しないシュレディンガー方程式

\[\left( -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} +V(x) \right) \varphi (x)=E \varphi (x)\]

を解くことによって

を調べてみましょう。

あわせて読みたい

高校生でもわかるシュレディンガー方程式の導出と存在確率の求め方 時間依存しないシュレディンガー方程式と確率密度関数について高校生でもわかるようにわかりやすく解説します。

井戸の内側の波動関数を求める

まず井戸の外側，すなわち \(x<0,\; a<x\) の範囲では粒子は存在しないので，従ってこの範囲では \(\varphi (x)=0 \) になります。

一方，\(0<x<a \) のときシュレディンガー方程式は \(V(x)=0\) より

\[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\varphi (x)=E \varphi (x)\]

となります。これより，見やすくするために \[E=\frac{\hbar^2 k^2}{2m}, \quad \text{i.e.} \quad k=\frac{\sqrt{2mE}}{\hbar}\] とおくと元の式は

\[\frac{d^2}{dx^2} \varphi (x)=-k^2 \varphi (x)\]

となり，これは典型的な調和振動子の運動方程式であるので簡単に解くことが出来ますね。実際に，この式の一般解は \(A,B \) を任意の定数として

\[\varphi (x) =A \sin kx +B \cos kx\]

で書くことができます。

あわせて読みたい

定数係数２階線形微分方程式の解き方を紹介 わかりやすい定数係数２階線形微分方程式の解き方を例題を併せて紹介します。

境界条件を考える

いま，波動関数 \(\varphi (x)\) の一般解が求まったので，境界条件から係数 \(A,B\) を求めてみましょう。ここでは境界条件

\[\varphi (0)= \varphi (-a)=0\]

を課すことによって波動関数を考えます。実際にこの条件から \[B=0, \; A \sin ka=0 \quad \text{i.e.} \quad ka=n\pi \quad (n=1,2,\cdots)\] が求まり，これより波動関数は

\[\varphi_n (x) =A \sin \frac{n \pi}{a}x \quad (n=1,2,\cdots)\]

と求めることができます。

関数を規格化する

次に波動関数を規格化し，係数 \(A\) を具体的に求めます。

【規格化の計算】
\[ \begin{align}
&\int_{0}^{a} |\varphi_n (x)|^2 dx =\int_{0}^{a} \left|A \sin \frac{n \pi}{a}x \right|^2 dx \\
&=|A|^2 \int_{0}^{a} \sin^2 \frac{n \pi}{a}x \; dx \\
&=\frac{|A|^2}{2}\int_{0}^{a} \left(1- \cos \frac{2n \pi}{a}x \right) dx \\
&=\frac{|A|^2}{2}\left(a- \int_{0}^{a} \cos \frac{2n \pi}{a}x \right) dx \\
&=\frac{1}{2}|A|^2 a=1
\end{align} \] よって \[A=\sqrt{\frac{2}{a}}\]

これより，井戸型ポテンシャルの具体的な波動関数は

\[\varphi_n (x)=\sqrt{\frac{2}{a}} \sin \frac{n \pi}{a}x \quad (n=1,2,\cdots)\]

と求めることが出来ました。

確率分布はどのようになるのか

波動関数は求まりましたが，実際にどのような振る舞いをするのでしょうか。例として具体的に \(n=1,2,3\) で確率密度関数 \(|\varphi_n (x)|^2\) を求めグラフにプロットしてみます。

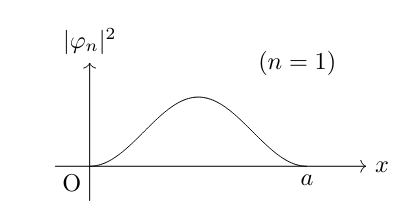
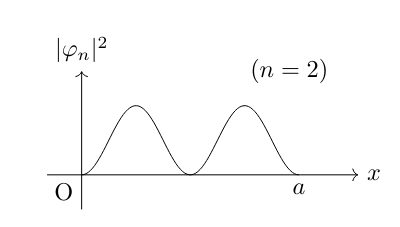
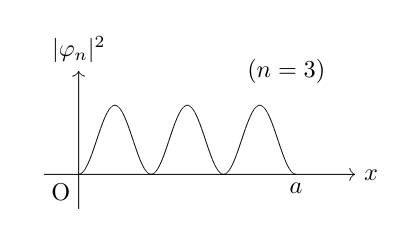
弾性衝突を繰り返す古典力学とは違い，粒子は上の図のように等間隔に分布していくことがわかります。

粒子のエネルギーを求める

波動関数が求まったので粒子のエネルギー \(E_n\) も求めてみましょう。\(ka=n\pi\) および \(\displaystyle E=\frac{\hbar^2 k^2}{2m}\) から自分で置いた文字 \(k\) を消去すると粒子のエネルギー

\[E_n=\frac{\hbar^2 k^2}{2m}=\frac{\hbar^2 \pi^2}{2ma^2}n^2\]

を求めることが出来ます。