極形式の意味と使い方と具体例のまとめ【例題あり】

2024年4月2日2024年12月24日

極形式\[z=r(\cos \theta + i \sin \theta)\] の定義や意味，極形式への変換方法と計算問題をまとめます。

極形式の導入

複素数平面では，$i$ を回転の作用を持つものとして考え導入しました。

しかし，回転に関する議論をしたいときに従来の複素数の形 \[z=a+bi\] とおいているのでは複素数の良さが発揮出来ない問題があります。そこで，回転に都合の良いように座標を取るため \[z=r(\cos \theta + i \sin \theta)\] の形で複素数 $z$ を表す方法を導入します。

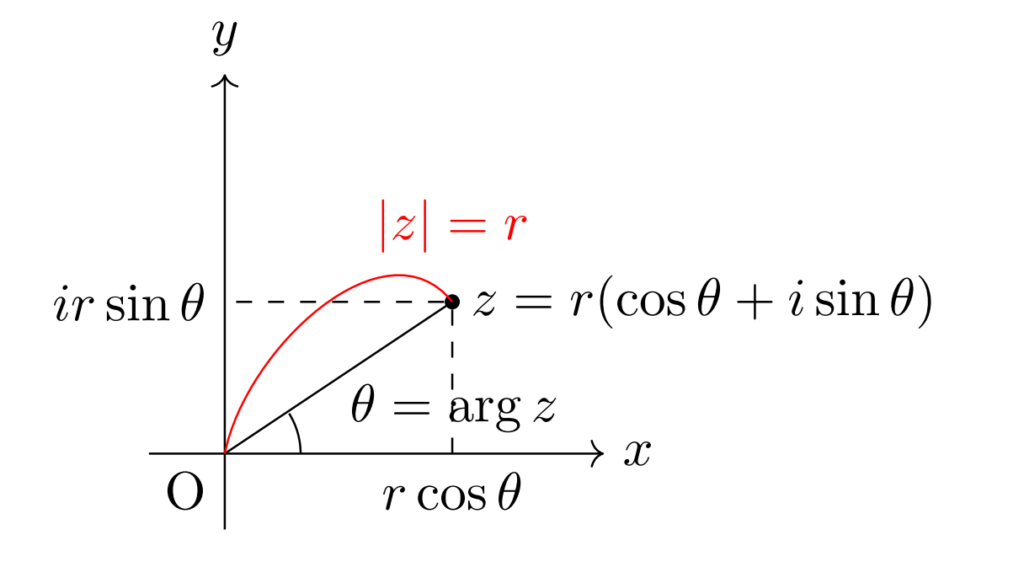
このような $z$ の表し方を $z$ の極形式といいます。また，このときの $\theta$ を $z$ の偏角といい，$\arg z$ で表します。

あんとら

$\arg z$ の表し方は１つには定まらないので，通常 $0 \leqq \arg z < 2\pi$ や $-\pi \leqq \arg z < \pi$ といった形で範囲の指定をされることが多いです

$z=a+bi$ と比較すると極形式の表示は \[a=r\cos \theta,\;b=r\sin \theta\] でおいたものとして見ることが出来るので複素数の絶対値 $|z|$ は \[\begin{align} |z| &=\sqrt{a^2+b^2} \\ &=\sqrt{r^2\cos^2 \theta+r^2\sin^2 \theta} \\&=r\sqrt{\cos^2 \theta+\sin^2 \theta} \\&=r \end{align}\] がわかります。

例題１

$z=2+2\sqrt{3}i$ を極形式で表し，複素平面上に図示しなさい。ただし $0 \leqq \arg z < 2\pi$ とする。

解答

$|z|=\sqrt{2^2+(2\sqrt{3})^2}=4$ であることに注意して求めると \[\begin{align} z &=4\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i \right) \\ &= 4 \left( \cos \frac{\pi}{3} +i\sin \frac{\pi}{3}\right) \end{align}\] また，図示すると次の通り。

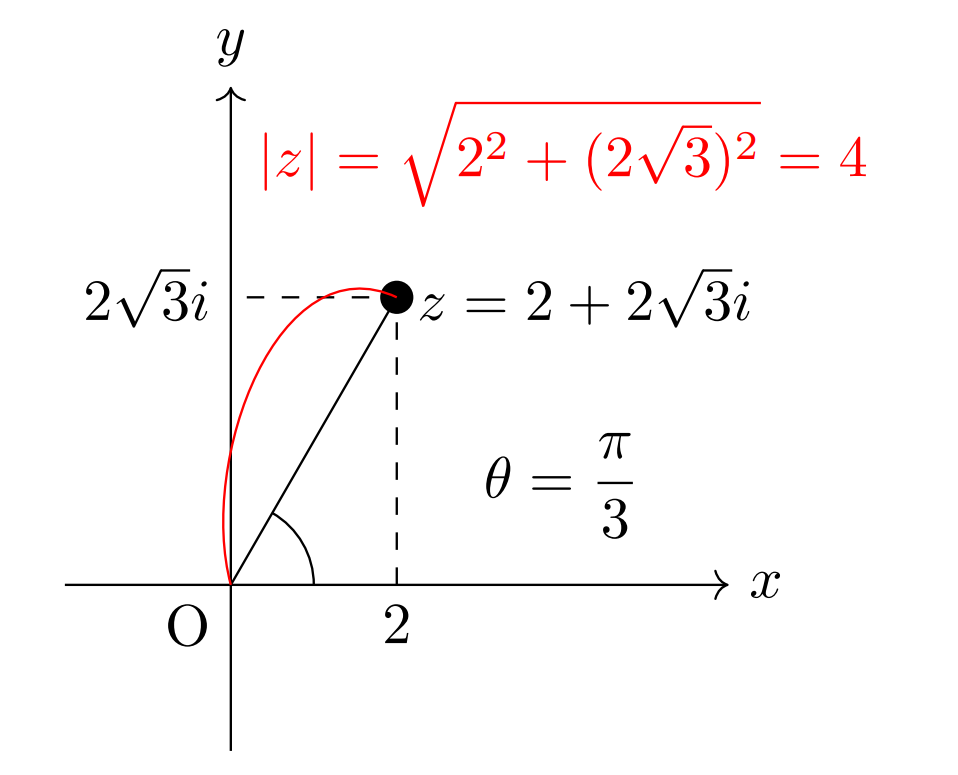
極形式表示による複素数の積と商

複素数 $z_1,z_2$ が極形式の形 \[z_1=r_1(\cos \theta_1 + i \sin \theta_1),\; z_2=r_2(\cos \theta_2 + i \sin \theta_2)\] で表されているときの積と商について以下が成り立ちます。

複素数 $z_1,z_2$ が極形式の形 \[z_1=r_1(\cos \theta_1 + i \sin \theta_1) \\ z_2=r_2(\cos \theta_2 + i \sin \theta_2)\] で表されているときの積と商について以下が成り立ちます。

極形式の重要性質まとめ

複素数 $z_1,z_2$ について

極形式の積の絶対値は絶対値 $r_1,r_2$ の積，すなわち \[|z_1 z_2|=r_1 r_2\]
極形式の積は偏角の和で計算できる。すなわち \[\arg (z_1 z_2)=\arg z_1 + \arg z_2\]
極形式の商の絶対値は絶対値 $r_1,r_2$ の商，すなわち \[\frac{z_1}{z_2}=\frac{r_1}{r_2}\]
極形式の商は偏角の差で計算できる。すなわち \[\arg \frac{z_1}{z_2}=\arg z_1 -\arg z_2\]

証明(というかただの計算)は次のように出来ます。

【積 $z_1 z_2$ の計算】
積 $z_1 z_2$ を計算すると \[\begin{align}z_1 z_2 &=r_1(\cos \theta_1 + i \sin \theta_1) \cdot r_2(\cos \theta_2 + i \sin \theta_2) \\ &=r_1 r_2 \{(\cos \theta_1 \cos \theta_2 -\sin \theta_1 \sin \theta_2) +i(\sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2)\} \\ &= r_1 r_2 \{\cos (\theta_1+\theta_2)+i\sin(\theta_1+\theta_2) \}\end{align}\] となり，極形式の積は偏角の和になることがわかる。

【商 $z_1/ z_2$ の計算】
商 $z_1 /z_2$ を計算すると \[\begin{align}\frac{z_1}{z_2} &= \frac{r_1(\cos \theta_1 + i \sin \theta_1)}{r_2(\cos \theta_2 + i \sin \theta_2)} \\ &= \frac{r_1(\cos \theta_1 + i \sin \theta_1)(\cos \theta_2 -i \sin \theta_2)}{r_2(\cos \theta_2 + i \sin \theta_2)(\cos \theta_2 -i \sin \theta_2)} \end{align}\] ここで，分母は \[\begin{align} & r_1\{(\cos \theta_1 \cos \theta_2 +\sin \theta_1 \sin \theta_2) +i(\sin \theta_1 \cos \theta_2 -\cos \theta_1 \sin \theta_2)\} \\ &=r_1 \{\cos (\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\} \end{align}\] 分子は \[r_2 (\cos^2 \theta_2 +\sin^2 \theta_2) =r_2\] であるので \[\frac{z_1}{z_2}=\frac{r_1}{r_2}\{\cos (\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\}\] となり，極形式の商は偏角の差になることがわかる。

あんとら

積を偏角の和で計算できる，ということはとても凄い性質で，複素数の持つ利点の１つです！

この性質により点の回転操作が簡単に出来るようになります

例題２

３つの複素数 \[z_1=2\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right),\;z_2=\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right),\;z_3=3\left(\cos \frac{3\pi}{4}+i\sin \frac{3\pi}{4}\right)\] について積 $z_1 z_2 z_3$ を計算しなさい。

３つの複素数 \[z_1=2\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right),\\ z_2=\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right),\\ z_3=3\left(\cos \frac{3\pi}{4}+i\sin \frac{3\pi}{4}\right)\] について積 $z_1 z_2 z_3$ を計算しなさい。

解答

偏角の和を計算すると \[\arg (z_1 z_2 z_3 )=\frac{\pi}{4}+\frac{\pi}{2}+\frac{3\pi}{4}=\frac{3\pi}{2}\] 絶対値の積は $r_1 r_2 r_3 =6$ より \[\begin{align}z_1 z_2 z_3 &=6 \left(\cos \frac{3\pi}{2}+i\sin \frac{3\pi}{2}\right) \\ &=-6i\end{align}\]