様々な計算の拡張となる複素数の概念と,複素平面上における基本事項をまとめます。
複素数の定義
\(i\) を虚数単位(\(i^2=-1\)),\(a,b\; (b \neq 0)\) を実数とするとき \[z=a+bi \] の形で表される数を複素数といいます。
このとき \(a\) を \(z\) の実部といい \(\text{Re} \; z=a\) と表します。また,\(b\) を \(z\) の虚部といい \(\text{Im} \; z =b\) と表します。
\(z=5+2i\) のとき \(\text{Re} \; z=5\),\(\text{Im} \; z =2\) である。
複素数と複素平面の対応
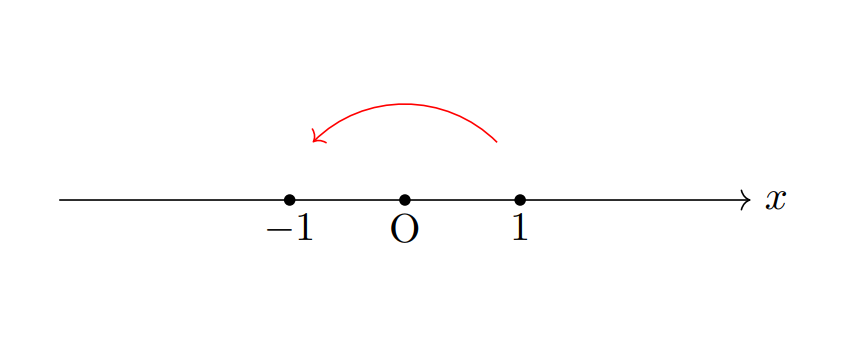
複素平面と実数の数直線上における対応を考えてみます。
いま,上の図において,1→-1への対応を考えると,0を基準として180度回転させていることがわかりますね。
ここで, \(i\) は \(i^2=-1\),すなわち2回かけると-1に移動することから,次のように \(y\) 軸を導入すると自然に拡張出来ます。
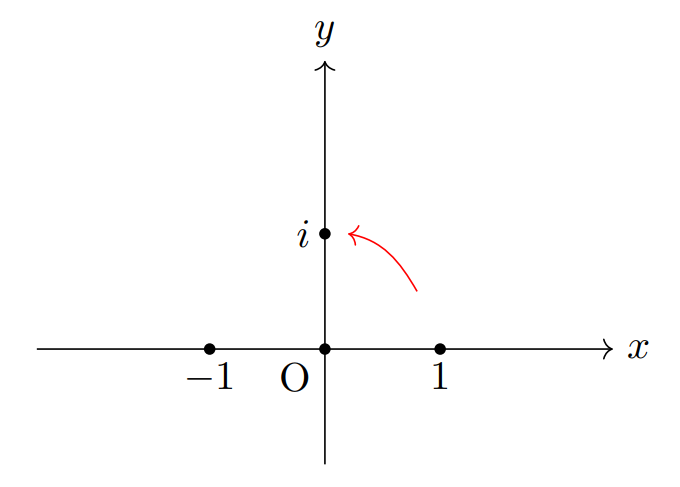
また,任意の複素数は \(z=a+bi \;(b \neq 0)\) とおけたので,図のように,\(a,b\) をそれぞれ \(x\) 軸,\(y\) 軸に対応させることができます。
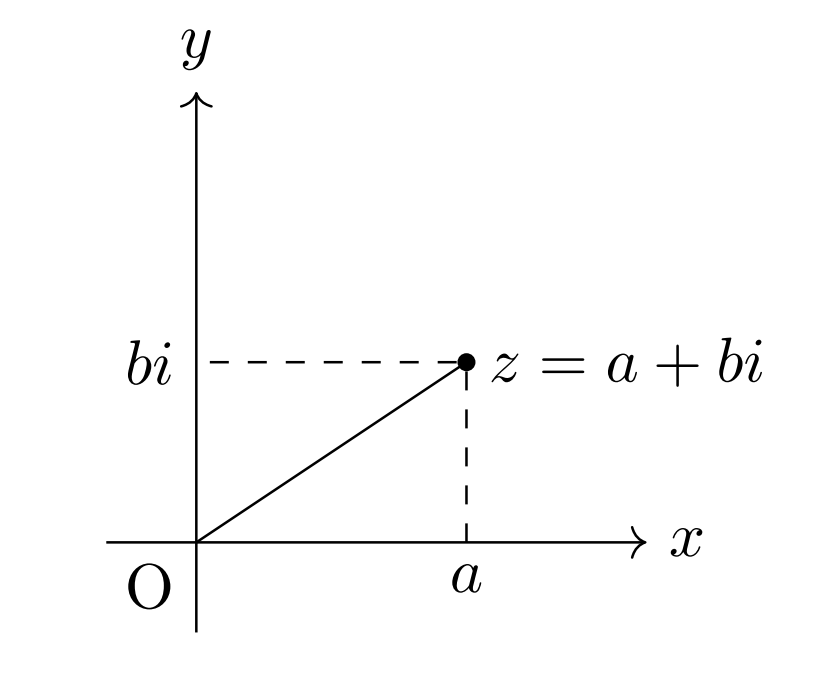
このようにして考えられる座標平面を複素数平面(またはガウス平面)といいます。
以下の複素数を複素数平面上に表しなさい。\[-1,\quad 2+i, \quad \overline{2+i}\]
\(\overline{2+i}=2-i\) であることに注意して複素数平面上に各々の複素数を図示すると次の通り。
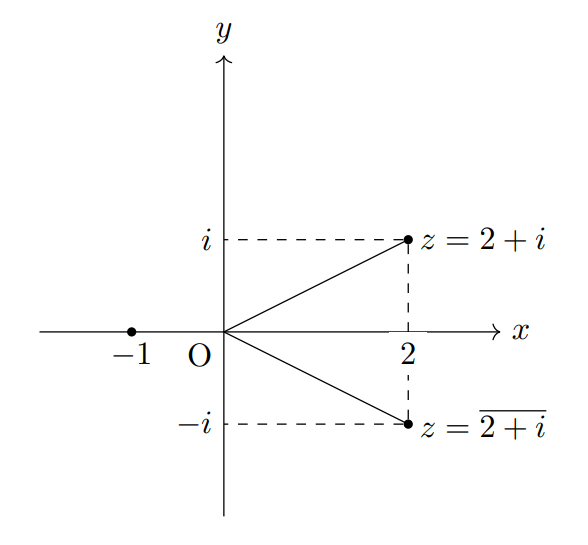
複素数の基本演算
複素数の基本演算は次のように行うことが出来ます。
\(a,b,c,d\) を実数とし2つの複素数を \(z_1 =a+bi\),\(z_2 =c+di\) とすると
- 複素数の和 \(z_1 +z_2\) は \[\begin{align} z_1 +z_2 &=(a+bi)+(c+di) \\ &=(a+c)+(b+d)i \end{align}\]
- 複素数の差 \(z_1 -z_2\) は \[\begin{align} z_1 +z_2 &=(a+bi)-(c+di) \\ &=(a-c)+(b-d)i \end{align}\]
- 複素数の積 \(z_1 z_2\) は \[\begin{align} z_1 z_2 &=(a+bi)(c+di) \\ &= ac+adi+bci-bd \\ &=(ac-bd)+(ad+bc)i \end{align}\]
- 複素数の商 \(\displaystyle \frac{z_1}{z_2}\) は \[\begin{align} \frac{z_1}{z_2} &=\frac{a+bi}{c+di} \\ &= \frac{(a+bi)(c-di)}{(c+di)(c-di)} \\ &=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2} \\ &= \frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i \end{align}\]
特に割り算の場合は上の通り,分母に共役な複素数 \[\overline{z}=\overline{c+di}=c-di\] を分母と分子にかけることで分母を実数にします。
複素数の絶対値
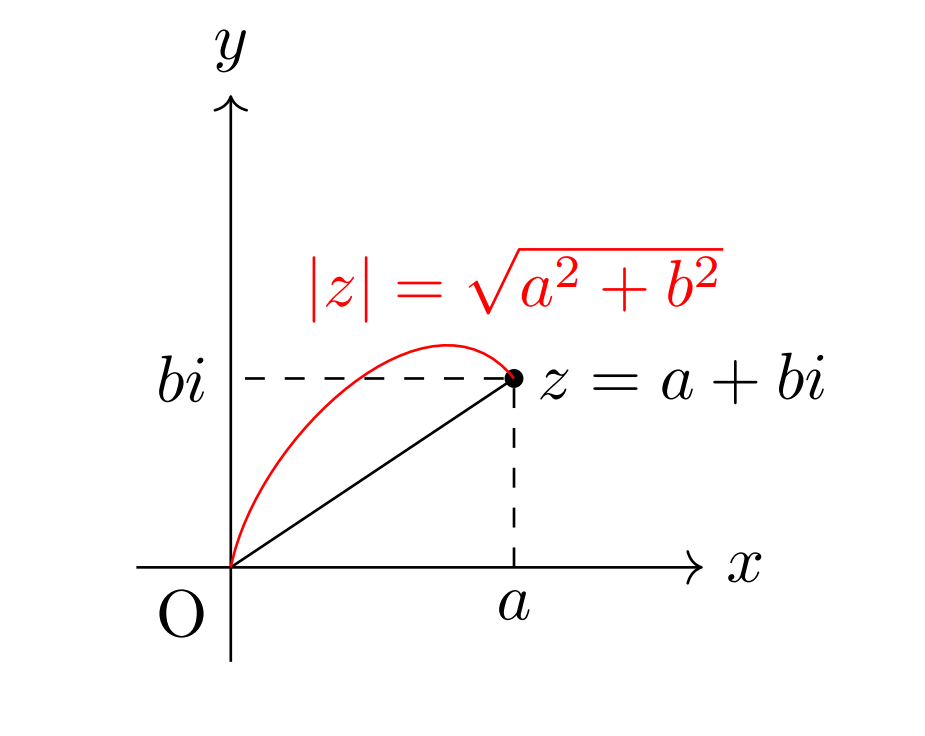
複素数を \(z=a+bi\) とおくと,図より複素数の絶対値は原点Oとの距離として \[|z|=\sqrt{a^2+b^2}\] と表すことが出来ます。
2点間の距離
同様に考えることによって,2つの複素数 \(z_1 =a+bi\),\(z_2 =c+di\) の距離は \[|z_1-z_2|=\sqrt{(a-c)^2+(b-d)^2}\] と表すことが出来ます。
複素平面上における円の方程式
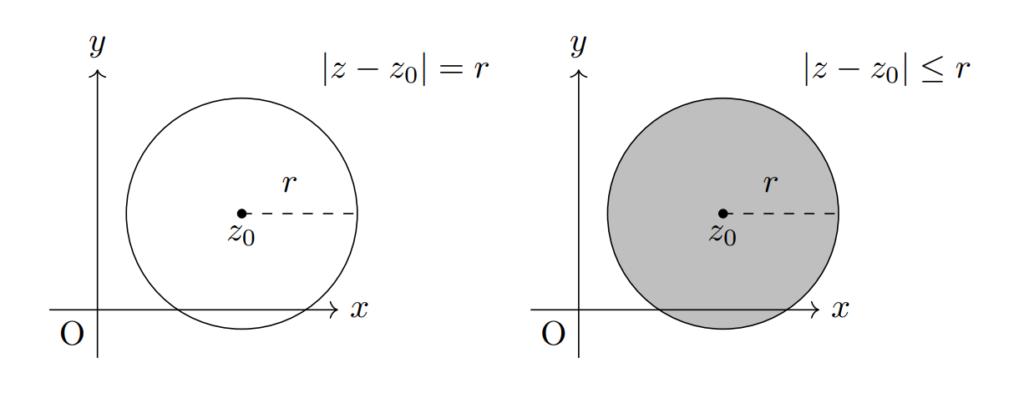
いま,\(|z_1-z_2|\) は2点 \(z_1,z_2\) の距離を表したので,正の実数 \(r\) と定点 \(z_0\) に対して \[|z-z_0|=r\] は \(z_0\) からの距離が \(r\) である \(z\) の集合,すなわち \(z_0\) を中心とした半径 \(r\) の円を表します。また,\[|z-z_0| \leq r\] とすると,\(z_0\) を中心とした半径 \(r\) の円の内部を表すことも出来ます。
 あんとら
あんとら複素平面上では円を簡単に表すことが出来ます
次の等式,不等式が表す複素平面上の点 \(z\) を図示しなさい。
(1) \(|z|=1\) (2) \(\displaystyle |z-(1+i)|<\frac{1}{2}\)
それぞれ図示すると次の通り。ただし (2) は境界線を含まない。
(1)
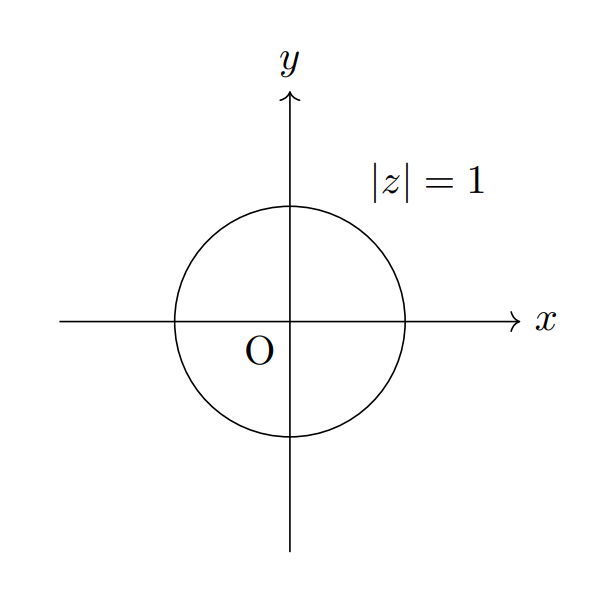
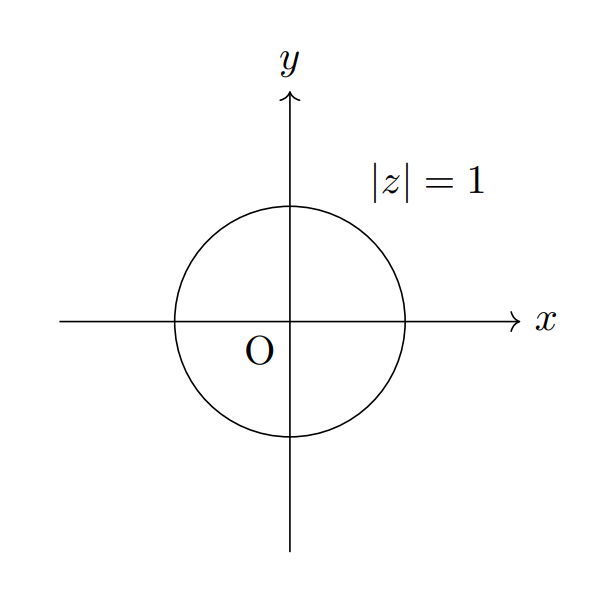
(2)
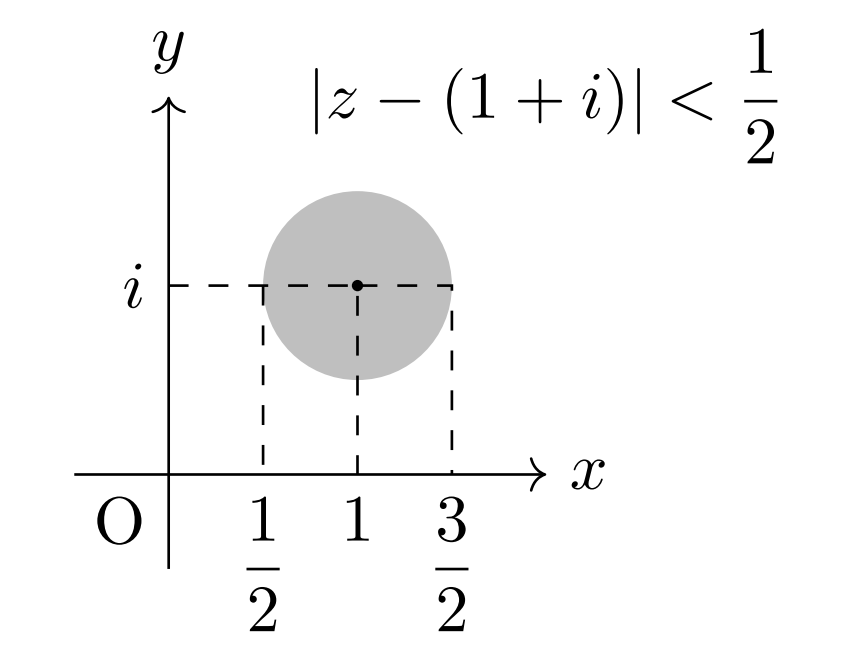
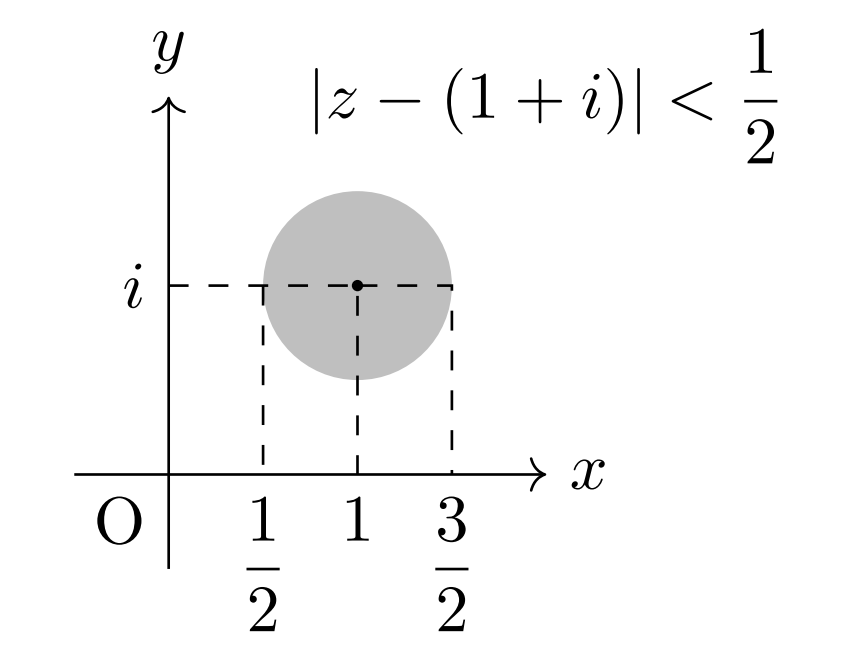


コメント