ガウス積分の導出と頻出の積分公式５つ・使用例の紹介

2023年11月18日2024年12月11日

統計力学や量子力学の計算で頻出であるガウス積分\[\int_{-\infty}^{\infty} e^{-ax^2}dx\] について，導出と積分公式，及びその導出を紹介します。

ガウス積分とは

$a$ を実数とし，$e^{-ax^2}$ の $[-\infty,\infty]$ における積分\[\int_{-\infty}^{\infty} e^{-ax^2}dx\] をガウス積分といいます。この積分は大学の微積分学で習う典型的な広義積分の１つであり，量子力学や統計学など様々な場面でしばしば現れます。

（参考）$y=e^{-ax^2}$ のグラフ

$y=e^{-ax^2}$ のグラフを図示すると次のようになります（グラフでは $a=1$ としています）。

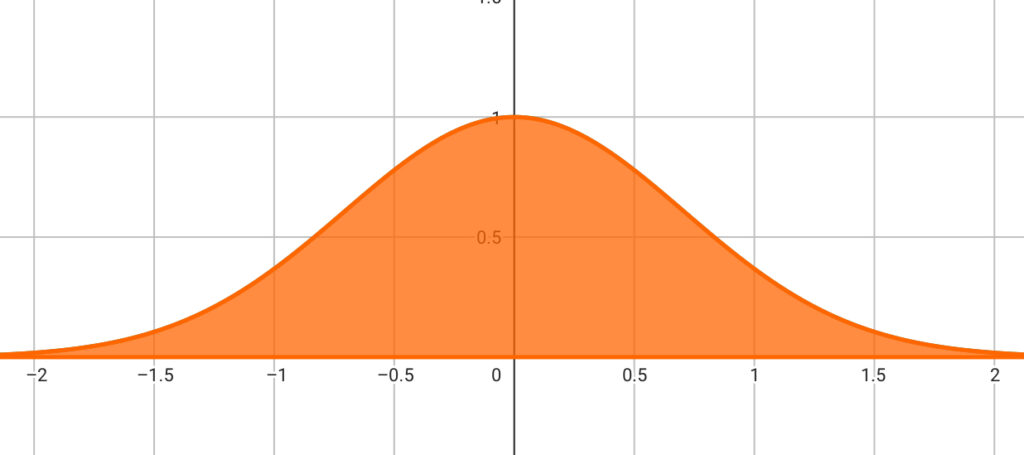
ガウス積分とは，図の橙色で囲まれた部分の面積を求めることであり，結論を先に書いてしまうと，その値は $\displaystyle \sqrt{\frac{\pi}{a}}$ になります。

また，$y=e^{-ax^2}$ は偶関数であるので，特に $a=1$ のとき \[\int_{0}^{\infty} e^{-x^2} dx= \frac{\sqrt{\pi}}{2}\] であることもわかりますね。以下ではこの結果について証明しましょう。

ガウス積分の導出

ガウス積分の計算では少々天下りではありますが，まず \[ I=\int_{-\infty}^{\infty} e^{-ax^2}dx\] と，この積分を $x$ から $y$ に変数変換した積分 \[ I=\int_{-\infty}^{\infty} e^{-ay^2}dy\] を用意します。この２つの積分は文字が違うだけなので値が変わることはありません。

そして，これら２つを掛け合せたもの \[ I^2=\int_{-\infty}^{\infty} e^{-a(x^2+y^2)}dxdy\] について，極座標変換 $x=r \cos \theta,y=r \sin \theta$ を考え，計算を進めます。このとき \[dxdy=rdr d\theta\] と出来ます。また積分区間について，$x,y$ の積分区間が $0 \to \infty$ のとき，$r$ の積分区間は $0 \to \infty$，$\theta$ の積分区間は $0 \to 2\pi$ となりますので，従って \[ \begin{align}
I^2 &=\int_{0}^{\infty} \int_{0}^{2\pi} e^{-ar^2}rdrd\theta \\
&= \int_{0}^{2\pi}d\theta \int_{0}^{\infty}e^{-ar^2}rdr
\end{align}\] と出来ます。これはそれぞれ独立に積分することが出来て \[
\int_{0}^{2\pi}d\theta =2\pi\] \[ \int_{0}^{\infty}e^{-ar^2}rdr =\left[ -\frac{e^{-ar^2}}{2a} \right]_{0}^{\infty}=\frac{1}{2a}
\] よって \[I^2 = \frac{\pi}{a}\] $I>0$ であることから

\[ I=\int_{-\infty}^{\infty} e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}\]

が示されました。

ガウス積分の重要公式とその証明

上のガウス積分程ではありませんが類題として次のような積分を使うこともあります。以下の計算過程も確認しましょう。

ガウス積分の公式

$a,b$ は正の実数とする。このとき次の関係が成り立つ

公式１ \[\int_{-\infty}^{\infty} e^{-a(x-b)^2}dx=\sqrt{\frac{\pi}{a}}\]
公式２ \[\int_{-\infty}^{\infty} e^{-ax^2+bx}dx=e^{\frac{b^2}{4a}} \sqrt{\frac{\pi}{a}}\]
公式３ \[\int_{-\infty}^{\infty} x^2e^{-ax^2}dx=\frac{1}{2a} \sqrt{\frac{\pi}{a}}\]
公式４ \[\int_{-\infty}^{\infty} x^{2n-1}e^{-ax^2}dx=0\]
公式５ \[\int_{-\infty}^{\infty} x^{2n}e^{-ax^2}dx=\frac{(2n-1)!!}{(2a)^n}\sqrt{\frac{\pi}{a}}\]

【１の証明】
$y=e^{-a(x-b)^2}$ のグラフは $y=e^{-ax^2}$ のグラフを $x$ 軸正方向に $b$ 移動させたものであるので，$[-\infty ,\infty]$ で積分した値は変わらない。したがって \[\int_{-\infty}^{\infty} e^{-a(x-b)^2}dx=\sqrt{\frac{\pi}{a}}\]
【２の証明】\[ -ax^2+bx=-a \left(x-\frac{b}{2a}\right)^2+\frac{b^2}{4a}
\] であるので \[ \begin{align}
&\int_{-\infty}^{\infty} e^{-ax^2+bx}dx \\ &=e^{\frac{b^2}{4a}}\int_{-\infty}^{\infty} e^{-a \left(x-\frac{b}{2a}\right)^2}dx =e^{\frac{b^2}{4a}}\sqrt{\frac{\pi}{a}} \end{align}\] よって \[\int_{-\infty}^{\infty} e^{-ax^2+bx}dx=e^{\frac{b^2}{4a}} \sqrt{\frac{\pi}{a}}\]
【３の証明】\[ \begin{align}
&\int_{-\infty}^{\infty} x^2 e^{-ax^2}dx
\\ &=\left[ -\frac{x}{2a}e^{-ax^2}\right]_{-\infty}^{\infty}+\int_{-\infty}^{\infty} \frac{1}{2a}e^{-ax^2}dx
\\ &=\frac{1}{2a}\int_{-\infty}^{\infty} e^{-ax^2}dx
\\ &=\frac{1}{2a} \sqrt{\frac{\pi}{a}} \end{align}\] よって \[\int_{-\infty}^{\infty} x^2e^{-ax^2}dx=\frac{1}{2a} \sqrt{\frac{\pi}{a}}\]
【４の証明】
$x^{2n-1}$ は奇関数，$e^{-ax^2}$ は偶関数であるので $x^{2n-1}e^{-ax^2}$ は奇関数である。積分区間は $[-\infty ,\infty]$ であるので，この積分は 0 となる。よって \[\int_{-\infty}^{\infty} x^{2n-1}e^{-ax^2}dx=0\]
【５の証明】\[
I_n=\int_{-\infty}^{\infty} x^{2n}e^{-ax^2}dx\] とする。部分積分すると \[ \begin{align} &I_n =\left[ -\frac{x^{2n-1}}{2a} e^{-ax^2}\right]_{-\infty}^{\infty}+(2n-1) \int_{-\infty}^{\infty} \frac{x^{2n-2}}{2a}e^{-ax^2}dx
\\ &=\frac{2n-1}{2a}I_{n-1}
\\ &=\frac{(2n-1)\cdot(2n-3)\cdot \cdots \cdot 2 \cdot 1}{(2a)\cdot(2a)\cdot \cdots \cdot (2a)}I_0
\\ &=\frac{(2n-1)!!}{(2a)^n} \int_{-\infty}^{\infty} e^{-ax^2}dx
\\ &=\frac{(2n-1)!!}{(2a)^n}\sqrt{\frac{\pi}{a}} \end{align}\] よって \[\int_{-\infty}^{\infty} x^{2n}e^{-ax^2}dx=\frac{(2n-1)!!}{(2a)^n}\sqrt{\frac{\pi}{a}}\]