グランドカノニカル分布の様々な物理量の導出方法

この記事ではグランドカノニカル分布における様々な物理量の導出方法をまとめます。

グランドカノニカル分布とは

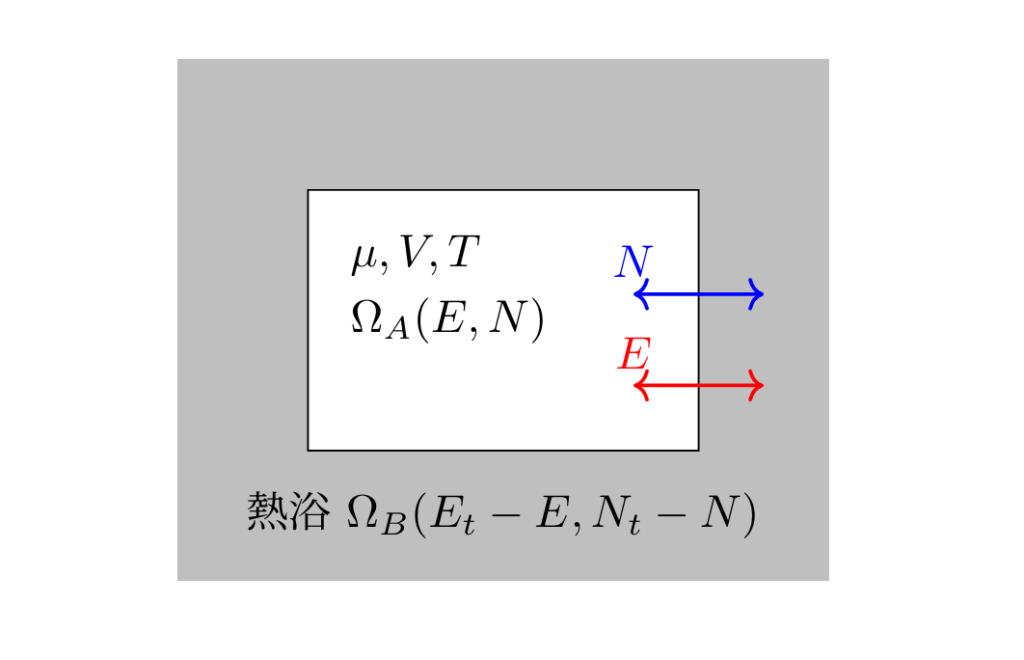
大分配関数の導出に入る前にまずはグランドカノニカル分布（大正準集団）と呼ばれる系についてまとめます。

グランドカノニカル分布とは，通常 化学ポテンシャル \(\mu\)，体積 \(V\)，温度 \(T\) が固定された集団のことを示します。

外部に接している熱浴とエネルギーのやりとりだけでなく，粒子数 \(N\) の交換が起こっている，ということが特徴ですね。

また，この系で重要なものとして次で表される大分配関数と呼ばれるものがあります。\[\begin{align} \Xi &=\sum_{N=0}^{\infty}\sum_{i=1}^{\infty} \exp \left( -\frac{E_i}{k_B T}+\frac{\mu N}{k_B T} \right) \\ &=\sum_{N=0}^{\infty}\sum_{i=1}^{\infty} e^{-\beta (E_i-\mu N)} \quad (\beta =\frac{1}{k_B T}) \end{align}\]

導出はこちら

あわせて読みたい

グランドカノニカル分布と特徴と大分配関数の導出方法【量子統計力学】 カノニカル分布とグランドカノニカル分布の違いや，グランドカノニカル分布における大分配関数の求め方についてわかりやすく紹介します。

ここではこの大分配関数について分配関数との関係を探りつつ，様々な物理量を計算します。

グランドカノニカル分布とカノニカル分布の関係

大分配関数の計算では基本的に粒子についての総和 \(N\) とエネルギーの状態 \(i\) について総和を取る必要があります。この際に\[\Xi=\sum_{N=0}^{\infty}e^{\beta \mu N} \sum_{i=1}^{\infty} e^{-\beta E_i} \]と書き直すと，カノニカル分布の分配関数 \[Z_C=\sum_{i=1}^{\infty} e^{-\beta E_i}\] を使うことが出来て，大分配関数 \(\Xi\) は

\[\Xi =\sum_{N=0}^{\infty}e^{\beta \mu N} Z_C\]

と分配関数 \(Z_C\) を用いて表すことが出来ます。

グランドカノニカル分布の平均の粒子数

グランドカノニカル分布における平均の粒子数 \(\overline{N}\) を求めます。\(\overline{N}\) を求めるときは天下り的ではありますが，次のように \(\log \Xi\) を \(\mu\) で微分します。すると\[\begin{align}\frac{d \log \Xi}{d \mu} &=\frac{1}{\Xi} \frac{d \Xi}{d \mu} = \frac{1}{\Xi} \frac{d}{d \mu} \sum_{N=0}^{\infty}e^{\beta \mu N} Z_C \\ &= \frac{\beta}{\Xi} \sum_{N=0}^{\infty}N e^{\beta \mu N} Z_C \\ &= \beta \overline{N} \end{align}\]従って，\(\beta =1/ k_B T\) と戻すと，グランドカノニカル系の粒子の平均値 \(\overline{N}\) は

\[\overline{N} = k_B T \frac{d \log \Xi}{d \mu} \]

と表すことが出来ます。

グランドカノニカル分布のエントロピー計算

次に，グランドカノニカル分布におけるエントロピー \(S\) を求めてみます。エントロピーの定義から

\[\begin{align}&S = -k_B \sum_{i,N} P_{i,N} \log P_{i,N} \\ &= -k_B \sum_{i,N}\frac{e^{-\beta (E_{i,N}-N\mu )}}{\Xi} \log \frac{e^{-\beta (E_{i,N}-N\mu )}}{\Xi} \\
&= -k_B \sum_{i,N}\frac{e^{-\beta (E_{i,N}-N\mu )}}{\Xi} (-\beta E_{i,N} +\beta \mu N -\log \Xi) \\
&= k_B \beta\color{red}{ \sum_{i,N} \frac{E_{i,N}e^{-\beta (E_{i,N}-N\mu )} }{\Xi}} -k_B \beta \mu \color{blue}{\sum_{i,N} \frac{ N e^{-\beta (E_{i,N}-N\mu )}}{\Xi}} +k_B \log \Xi \end{align}\]

ここで

ことからエントロピー \(S\) は\[S=\frac{E}{T}-\frac{\mu \overline{N}}{T}+k_B \log \Xi \] と求めることが出来ます。

他の物理量との関連

簡単にですが，他の熱力学関数との関連も調べておきましょう。熱力学関係式 \[pV=-E+ST+\mu \overline{N}\] を \(S\) について解いた式 \[S=\frac{E}{T}-\frac{\mu \overline{N}}{T}+\frac{pV}{T}\]と上のエントロピーの式を比較すると

\[pV=k_B T \log \Xi\]

であることがわかります。これより，圧力 \(p\) は \[p=k_B T \frac{\partial}{\partial V} \log \Xi \] と計算することも出来ます。

あわせて読みたい

吸着問題をグランドカノニカル分布を用いて解く方法 グランドカノニカル分布の典型的問題である吸着問題とそこから得られるラングミュアの吸着等温式について紹介します。

オススメ参考書