振動現象の1つである減衰振動について,運動方程式(微分方程式)とその解法について紹介します。
- 減衰振動の運動方程式の立式方法
- 運動方程式の解き方
- 抵抗力の大小による運動の変化の違い
減衰振動の運動方程式
減衰振動として次の系を考えます。
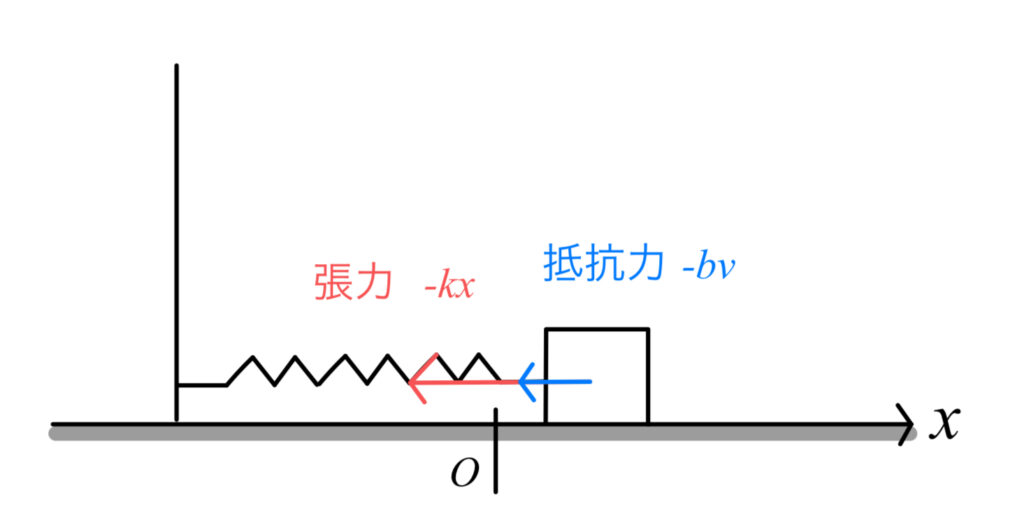
- 水平面内でばねに繋がれた物体の運動を考える
- ばねの自然長のときの物体の位置を \(x=0\)
- 物体の質量は \(m\)
- ばねの比例定数は \(k\)
- 物体にかかる空気抵抗の力は速度 \(v\) に比例し,このときの比例定数を \(-b\) ( \(b>0\) )
このとき,運動方程式は空気抵抗とばねの張力を足し合わせて
\[m\frac{d^2x}{dt^2}=-kx-bv\]
となります。
運動方程式を解く
運動方程式を解いてみましょう。
速度は位置の時間微分で与えられる,すなわち \(\displaystyle v = \frac{dx}{dt}\) であるので運動方程式に代入すると \[m\frac{d^2x}{dt^2}=-kx-b\frac{dx}{dt}\] ここですこし整理をします。\(\displaystyle \gamma=\frac{b}{2m}\),固有角振動数 \(\displaystyle \omega_0= \sqrt{\frac{k}{m}}\) とおいて移項すると \[\frac{d^2x}{dt^2}+2 \gamma \frac{dx}{dt} + \omega_0^2 x=0\] これは定数係数2階微分方程式になるので,特性方程式 \[\lambda^2+2\gamma \lambda+\omega_0^2=0\] の解が
- 実数解を2つ持つ
- 重解を持つ
- 複素数の解を持つ
の3つの場合にわけて考えることが出来ます。
 あんとら
あんとら\(\gamma\) は抵抗力の大きさを表しているので,物理的な場合分けとしては
① 抵抗力が大きいとき
② 抵抗力がばねの振動とちょうど釣り合うとき
③ 抵抗力が小さい時
として考えることが出来そうです
① 実数解を2つ持つとき(\(\gamma^2-\omega_0^2>0\))
特性方程式は2つの解 \[\lambda=-\gamma \pm \sqrt{\gamma^2-\omega_0^2}\] を持つので,微分方程式の解は \[x(t)=c_1 e^{-(\gamma – \sqrt{\gamma^2-\omega_0^2})t}+c_2e^{-(\gamma + \sqrt{\gamma^2-\omega_0^2})t}\] となります(\(c_1,c_2\) は定数)。
このときのグラフを図示すると次のようになります。
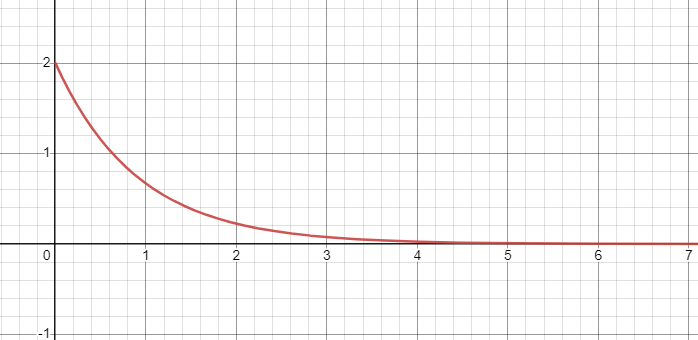

これより,空気抵抗の力が大きいとき,ばねの振動はそのまま止まってしまうことがわかります。
② 重解を持つとき(\(\gamma^2-\omega_0^2=0\))
特性方程式は重解 \(\lambda =-\gamma\) を持つので,微分方程式の一般解は \[x(t)=(c_1+c_2t)e^{-\gamma t}\] となります。
このときのグラフを図示すると次のようになります。
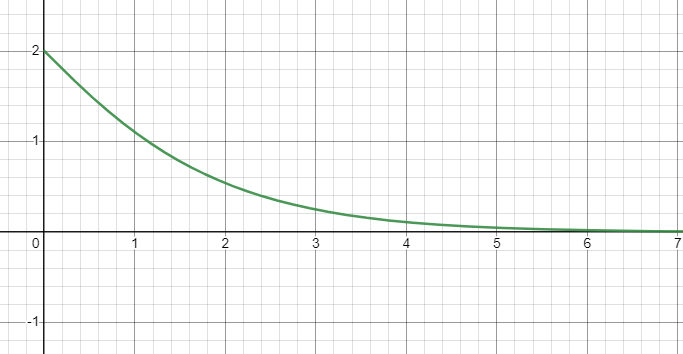

これより空気抵抗とばねの張力が釣り合うとき,①と同様ばねの振動はそのまま止まってしまうことがわかります(臨界減衰といいます)。
③ 複素数の解を持つとき(\(\gamma^2-\omega_0^2<0\))
\(\gamma^2-\omega_0^2<0\) のとき,特性方程式は複素数解 \[\lambda=-\gamma \pm \sqrt{\omega_0^2-\gamma^2}i\] を持つので,微分方程式は \[x(t)=e^{-\gamma t}[c_1 \sin (\sqrt{\omega_0^2-\gamma^2} t) + c_2 \cos (\sqrt{\omega_0^2-\gamma^2} t)]\] となります。
グラフに図示すると次のようになります。
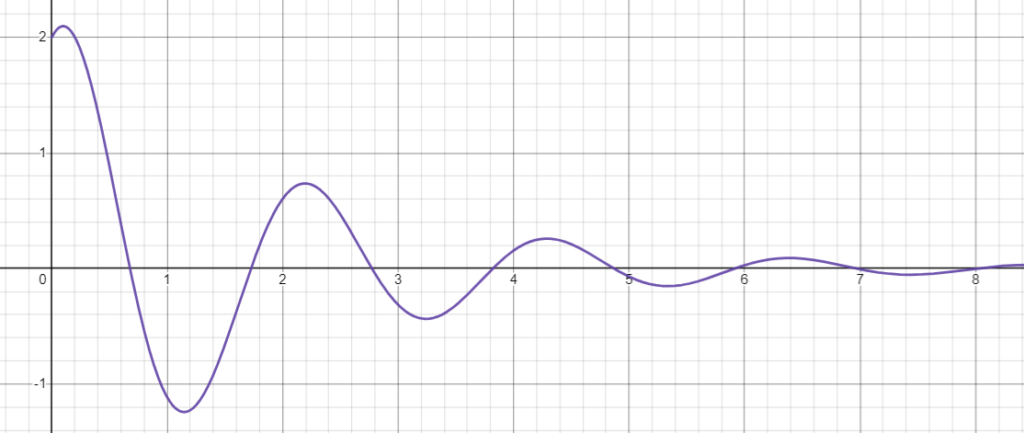

これより,物体は振動を次第に弱め,最終的に止まってしまうことがわかります。
このように,次第に振幅が小さくなりながら振動を繰り返す運動を「減衰振動」といいます。
まとめ
この記事では
- 減衰振動の運動方程式の立式方法
- 運動方程式の解き方
- 抵抗力の大小による運動の変化の違い
について紹介しました。参考になれば幸いです。


コメント