運動方程式って何？微積分を使った立式方法とその例題

2024年4月26日2025年1月7日

高校物理や大学物理で使われる運動方程式 \[m\frac{d^2 \boldsymbol{r}}{dt^2}=\boldsymbol{F}\] と運動方程式の使い方を微積分を用いつつ，実際に例題を用いて紹介します。

運動方程式とは

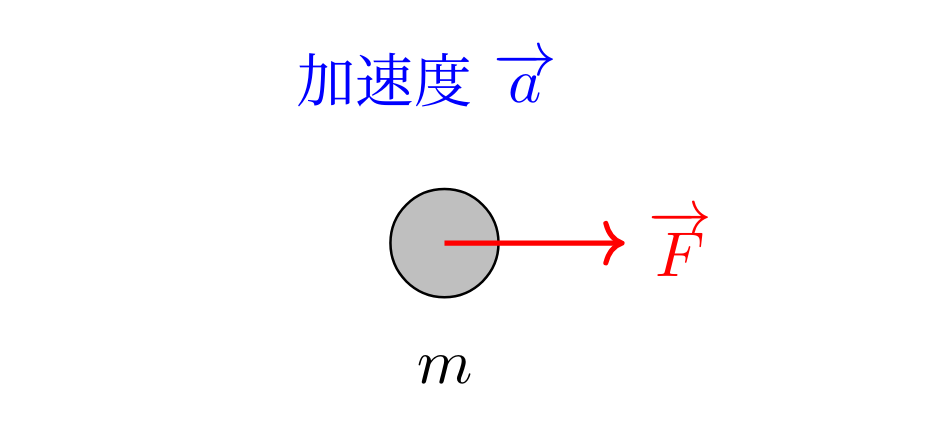
昔（17世紀後半くらい），ニュートンは実験で物体にある力 $\boldsymbol{F}$ を加えると，物体はその力の向きに，力に比例した加速度が生じる，物体の運動を数式で表すと \[\boldsymbol{a}=\frac{1}{m}\boldsymbol{F}\] となることを発見しました。ここで $\displaystyle \frac{1}{m}$ は比例定数であり，$m$ はこの式からその物体の質量と定義されます。加速度は変位の二階微分 $\displaystyle \frac{d^2 \boldsymbol{r}}{dt^2}$ であったことを用いると

\[m\frac{d^2 \boldsymbol{r}}{dt^2}=\boldsymbol{F}\]

と書けます。この式を運動方程式といい，以降の力学ではほぼすべてがこの第2法則を出発点として議論が進みます。是非覚えておきましょう。

運動方程式の使い方は次節で扱いますが，運動方程式を使うことによって，物体の加速度がわかり，加速度がわかるとトントン拍子に他の物理量(位置や速度)も求まる，ということを頭の何処かに入れておくと運用するうえで見通しが良いですね。

尚，力がつり合っているときも運動方程式は成り立ちます。このとき，物体の速度は変化しないので，$a=0$ になります。これは慣性の法則(運動の第一法則)に従っていると見ることも出来ますね。

運動方程式の使い方

運動方程式は物理の起点となる式！と言われても実際の扱いは些か難しいものがあると思われます。そこで，以下に運動方程式の具体的な使い方をまとめます。

STEP１：扱う物体にかかっている力をすべて把握（図示）する

まず，扱う物体にかかっているすべての力を書き出します。書き出す際に主に出てくる力は

重力
物体の垂直抗力
ばねの力や張力，空気抵抗 etc

があります。

STEP2：各方向ごとに力の成分の和を計算する

$x$ 軸方向，$y$ 軸方向ごとにこれらの成分を足し合わせ，$\boldsymbol{F}$ を求めます。

STEP３：運動方程式に代入し，加速度を求める

運動方程式の $\boldsymbol{F}$ にstep２で求めたものを代入し，加速度を求めます。

加速度を求めたら必要に応じて速度や位置を積分して求めます。尚，積分すると積分定数が現れますが，これを決定するためにはある時刻の速度 $\boldsymbol{v}_0$ や位置 $\boldsymbol{r}_0$ が与えられなくてはありません。これを初期条件といいます。

例題

運動方程式を微分演算子を使って書くと，運動方程式が単なる微分方程式の問題に帰着します。実際に例題を見てみましょう。

例題

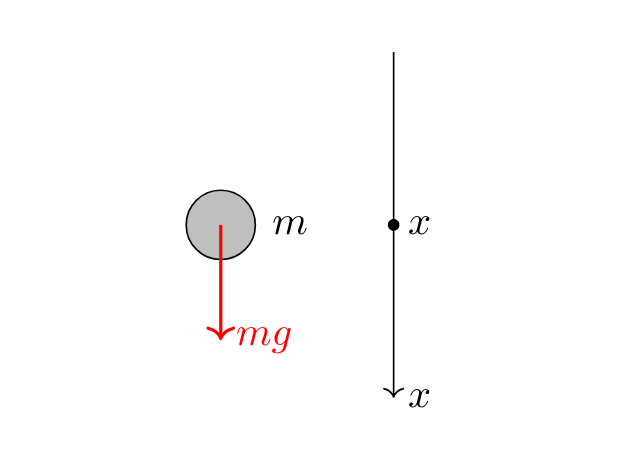
質量 $m$ の物体が原点から鉛直方向に自由落下させるとき，以下の問に答えよ。ただし，時刻 $t=0$ の位置を原点とし，運動方向を $x$ 軸正方向に取るものとする。

(1) 物体の運動方程式を書きなさい。

(2) 時刻 $t$ における物体の加速度 $a$ を求めなさい。

(3) 時刻 $t$ における物体の速度 $v$ を求めなさい。

(4) 時刻 $t$ における物体の位置 $x$ を求めなさい。

【解答】
(1) 物体にかかっている力の大きさは $mg$，向きは $x$ 軸正方向であるので，運動方程式は \[ma_x=mg\]
(2) (1) より $a_x=g$ であり，物体は $x$ 軸正方向に大きさ $g$ で等加速度運動を行う。

(3) 加速度は速度を時間微分したもの，すなわち $\displaystyle a=\frac{dv}{dt}$ であるので，\[\frac{dv}{dt}=g\] これを時刻 $t$ について積分すると\[
\int \frac{dv}{dt} dt= \int g dt
\] \[v=gt+C_0\] ただし，$C_0$ は定数である。ここで，時刻 $t=0$ において速度 $v=0$ であるので，上式に $(v,t)=(0,0)$ を代入し $C_0$ を求めると $C_0=0$ となる。よって，求める答えは \[v=gt\]
(4) 速度は位置を時間微分したもの，すなわち $\displaystyle v=\frac{dx}{dt}$ であるので \[\frac{dx}{dt}=gt\] これを時刻 $t$ について積分すると \[
\int \frac{dx}{dt} dt= \int gt dt
\] \[x=\frac{1}{2}gt^2+C_1\] ただし，$C_1$ は定数である。時刻 $t=0$ において物体は原点にいる，すなわち $x(0)=0$ であるので，$C_1$ を求めると $C_1=0$ を得る。これより，求める答えは \[x=\frac{1}{2}gt^2\]