運動量・力積の定義とその使い方・導入するメリットをわかりやすく

2024年5月1日2024年10月10日

この記事では運動量と力積 \[\boldsymbol{p}=m\boldsymbol{v},\quad \boldsymbol{I}=\int_{t_1}^{t_2} \boldsymbol{F} dt\] の定義と関係，およびこの２つの物理量を導入するメリットについて紹介します。

運動量と力積

運動量と力積の諸々の説明に入る前にまず先にこれらを定義するところから始めましょう。

運動量と力積の定義

質量 \(m\) の物体が速度 \(\boldsymbol{v}\) で移動しているとき \[\boldsymbol{p}=m\boldsymbol{v}\] で定義される \(\boldsymbol{p}\) をその物体の運動量（運動量ベクトル）という
物体に力 \(\boldsymbol{F}\) が時刻 \(t_1\) から \(t_2\) まで作用したとき \[\boldsymbol{I}=\int_{t_1}^{t_2} \boldsymbol{F} dt\] で定義される \(\boldsymbol{I}\) を力積という

ここで \(m,t\) はスカラー量ですが，\(\boldsymbol{v},\boldsymbol{p},\boldsymbol{F},\boldsymbol{I}\) はベクトル量であることに注意してください。

あんとら

情報として「向き」と「大きさ」の２つを持ちます

この定義から \(\boldsymbol{p}\) は物体の運動の具合を表した量，といえますね。簡単なものですが例を見てみましょう。

【例】
\(x\) 軸正方向に質量 1.0 kg の物体が速度 2.0 m/s で移動しているとき，この物体の運動量は \[p_x=1.0 \times 2.0 \;[\text{kg} \cdot \text{m/s}]=2.0\;[\text{kg} \cdot \text{m/s}]\]

運動量と力積の関係

運動量と力積の関係を捉えるために，まず運動方程式 \[m\frac{d^2 \boldsymbol{r}}{dt^2}=\boldsymbol{F}\] を運動量 \(\boldsymbol{p}=m \boldsymbol{v}\) を使って書き換えてみます。

速度と加速度には \[\frac{d \boldsymbol{v}}{dt}=\frac{d^2 \boldsymbol{r}}{dt^2}\] の関係が成り立ったので，これを用いると運動方程式は

\[m \frac{d\boldsymbol{v}}{dt}=\frac{d \boldsymbol{p}}{dt}=\boldsymbol{F}\]

と表すことが出来ます。この式を \([t_1,t_2]\) で \(t\) について積分すると \[\int_{t_1}^{t_2}m \frac{d\boldsymbol{v}}{dt}dt=\int_{t_1}^{t_2} \boldsymbol{F} dt\] 左辺は \(dt\) が消えて積分変数を \(\boldsymbol{v}\) に取ることが出来て，右辺は力積の定義から \[\int_{t_1}^{t_2}m d\boldsymbol{v}=m\boldsymbol{v}_2-m\boldsymbol{v}_1=\boldsymbol{I} \] 運動量の定義 \(\boldsymbol{p}=m\boldsymbol{v}\) より結局

\[\boldsymbol{p}_2-\boldsymbol{p}_1=\boldsymbol{I} \]

となり，これから運動量と力積には（運動量変化）＝（力積）の関係が成り立つことがわかります。

運動量保存則とその導出

上で定義した運動量 \(\boldsymbol{p}\) ですが，これには次のような便利な法則が成り立ちます。

運動量保存則

２つの質量が \(m_{\text{A}},m_{\text{B}}\) である物体 A，B について時刻 \(t_1\) における各々の速度をそれぞれ \(\boldsymbol{v}_{\text{A}1},\boldsymbol{v}_{\text{B}1}\)，時刻 \(t_2\) における速度を \(\boldsymbol{v}_{\text{A}2},\boldsymbol{v}_{\text{B}2}\) とすると \[m_{\text{A}} \boldsymbol{v}_{\text{A}1}+m_{\text{B}} \boldsymbol{v}_{\text{B}1}=m_{\text{A}} \boldsymbol{v}_{\text{A}2}+m_{\text{B}} \boldsymbol{v}_{\text{A}2}\] が成り立つ。これを運動量保存則という

証明しておきましょう。証明にあたっては相互作用を及ぼしあっている２物体 A，B を考えます。

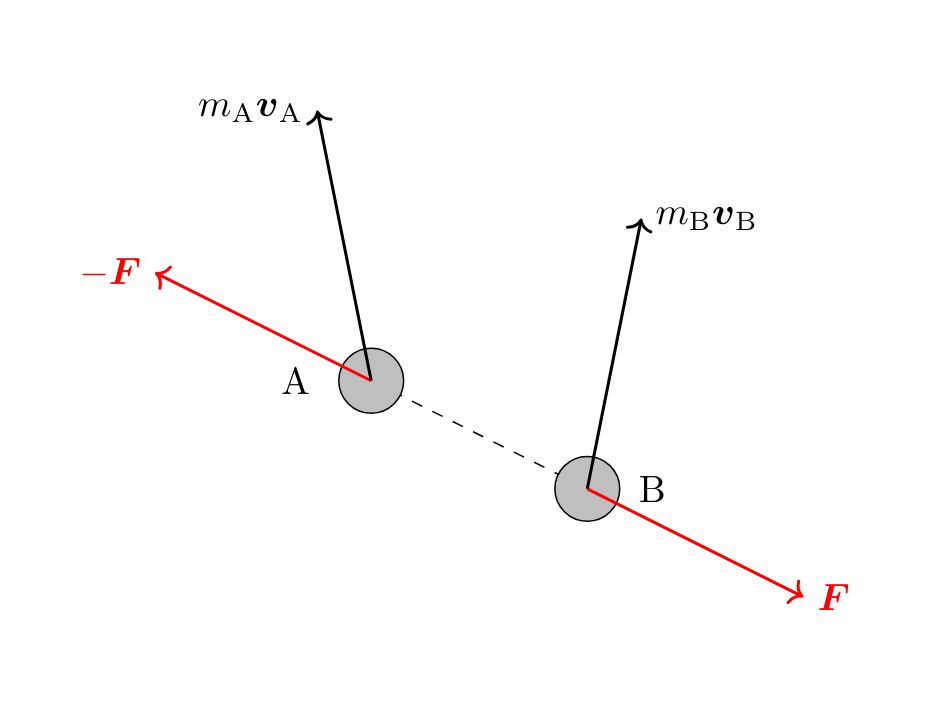
A が B に力 \(\boldsymbol{F}\) を及ぼしているとすると，B から A には反作用の法則から \(-\boldsymbol{F}\) がはたらきます。このとき時刻 \([t_1,t_2]\) において

【 A が B から受ける力積】 \[\int_{t_1}^{t_2} (-\boldsymbol{F}) dt=-\boldsymbol{I}\]
【 B が A から受ける力積】\[\boldsymbol{I}=\int_{t_1}^{t_2} \boldsymbol{F} dt\]

と書けるので上で得た上で得た関係式 \[m\boldsymbol{v}_2-m\boldsymbol{v}_1=\boldsymbol{I}\] をそれぞれに適用すると

【 A の運動量変化】\[m_{\text{A}} \boldsymbol{v}_{\text{A}2}-m_{\text{A}} \boldsymbol{v}_{\text{A}1}=-\boldsymbol{I}\]
【 B の運動量変化】\[m_{\text{B}} \boldsymbol{v}_{\text{B}2}-m_{\text{B}} \boldsymbol{v}_{\text{B}1}=\boldsymbol{I}\]

よりこれらを足し合わせて整理することにより運動量保存則

\[m_{\text{A}} \boldsymbol{v}_{\text{A}1}+m_{\text{B}} \boldsymbol{v}_{\text{B}1}=m_{\text{A}} \boldsymbol{v}_{\text{A}2}+m_{\text{B}} \boldsymbol{v}_{\text{A}2}\]

が成り立つことを示すことが出来ます。

運動量と力積を導入するメリット

力学的現象には様々な現象がありますが「衝突」という現象は現象としては身近であるにも関わらず，扱うには難しい現象です。

あんとら

極めて短時間に大きい力がはたらくので評価しづらい

そこで，力学では衝突の瞬間について具体的に議論するのではなく，衝突前後の物体の変化を見ることによって衝突の要素を見よう，としました。

例えばボールがバットに当たるような現象の力の時間変化は，横軸を時間 \(t\)，縦軸を力の大きさ \(F\) として次のように表すことが出来ます。

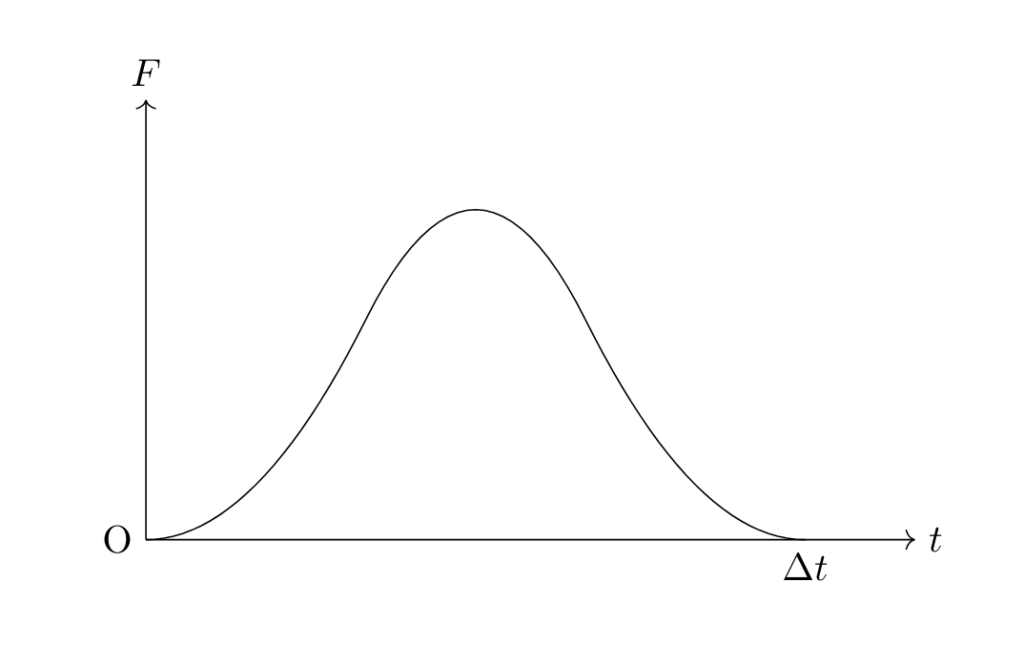
この面積部分が加えられた力の総量になりますが，このままでは計算が困難なので，次のように等積変形します。

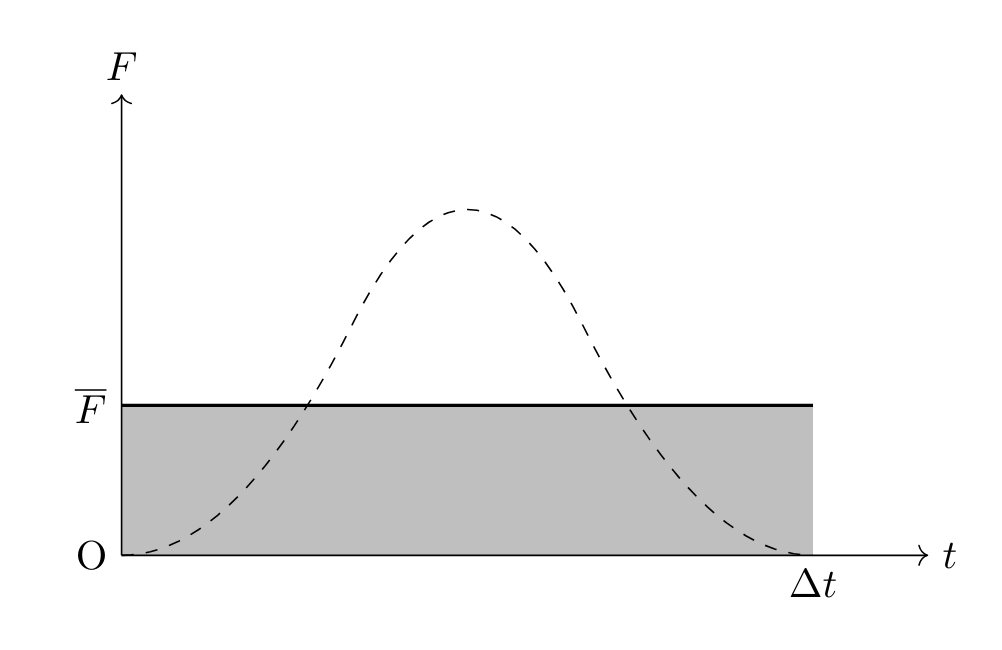
このようにすると受けたときの力積の大きさ（＝図の面積部分）は \[I=\overline{F} \Delta t\] より，\(\overline{F}\) は \[\overline{F}=\frac{I}{\Delta t}\] となって，瞬間的に働いた大きさを平均値として評価できるようになることがわかります。

つまるところ運動量と力積を導入するメリットとしては

反応前後を見るだけで衝突という短時間に大きい力がはたらく現象を評価することが出来るようになる

という点が挙げられます。

あんとら

反応の瞬間を見るのではなくその反応前後を見るという手法は運動量保存則の分野以外にも熱力学でも見られます

それゆえに運動量保存則は