地球からの万有引力を受けて運動する小球の問題(いわゆる「地球トンネル」問題)を紹介します。
地球トンネル問題
次のような系を考えます。
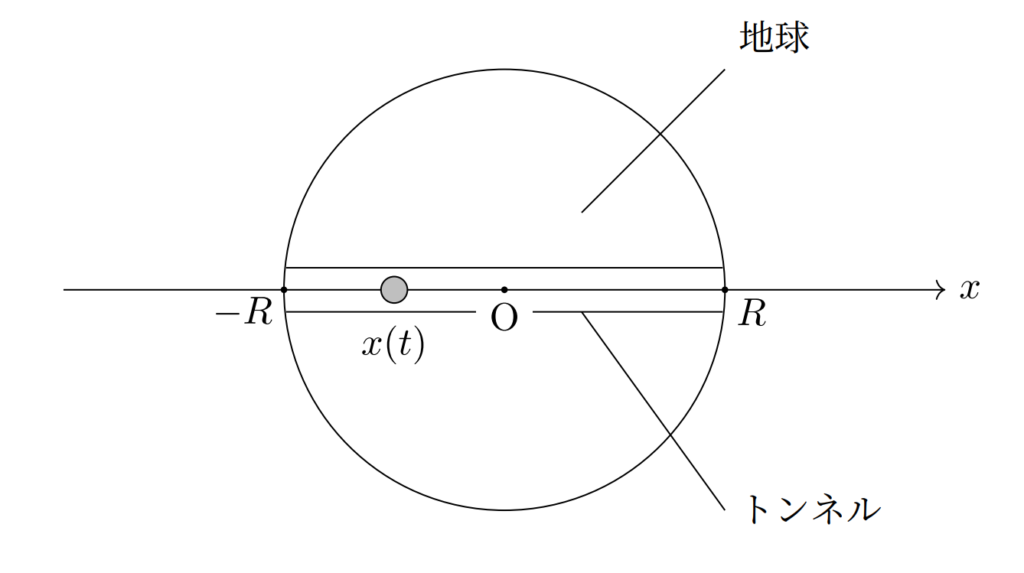
- 地球は点Oを中心とする質量 \(M\),半径 \(R\) の一様な密度の球
- 自転や公転,大気の影響は考えない
- トンネルは十分に細く,地球の質量の変化は無視できる
- 万有引力定数は \(G\)
- 時刻 \(t=0\) において質量 \(m\) の小球を \(x=R\) の地点から落とす
- 時刻 \(t\) における小球の位置を \(x=x(t)\),速度を \(v(t)\) とする
地球のある一点から地球の裏側まで掘り進め,トンネルを作ったときの運動の様子を見る問題です。
この設定のもとで,小球がどのような運動をするのか調べてみましょう。
小球の運動方程式
小球にはたらく万有引力の大きさは次の事実を使って調べることができます。
\(x=r \; (r<R)\) の位置にある小球が地球から受ける万有引力の大きさは中心Oから半径 \(r\) 内の球内の質量 \(M’\) が点Oに集まったとして,それと小球が受ける万有引力に等しい
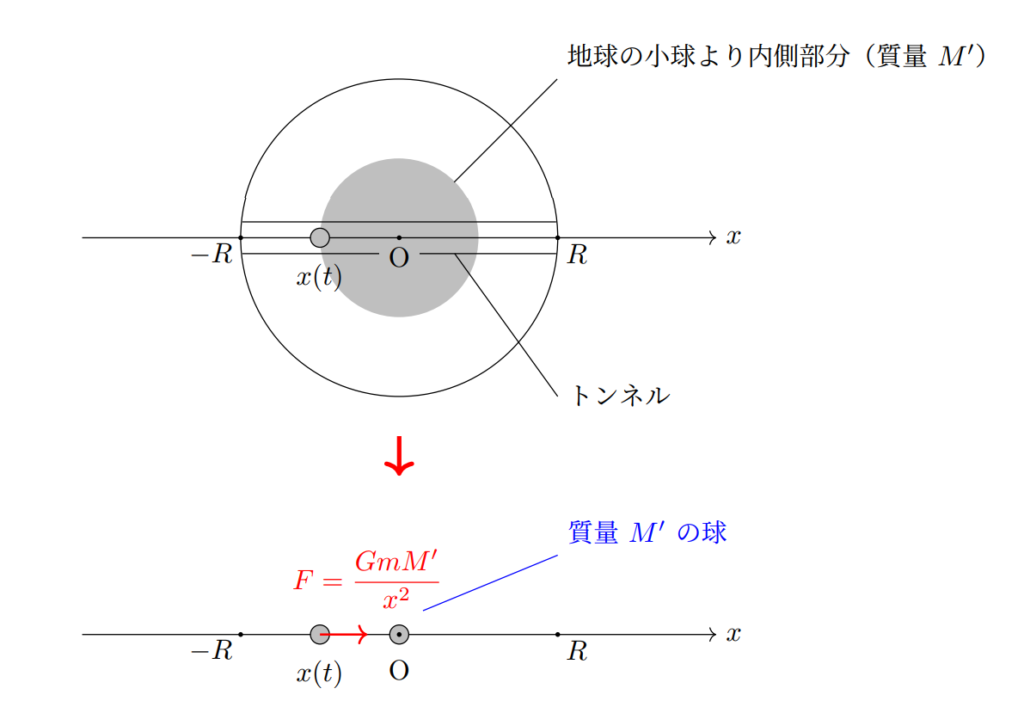
ここではこの事実を使って計算します。
\(M’\) の体積
小球にはたらく万有引力の大きさを求めるために,地球の中心Oから半径 \(x \; (x<R)\) の球内の質量 \(M’\) を求めます。
ここで,体積比は半径の3乗に比例するので \[ M’=\frac{x^3}{R^3}M\] と計算することができます。
万有引力の計算と運動方程式
上記より,小球にはたらく万有引力の大きさは \[ F= \frac{GmM’}{x^2} =\frac{GMm}{R^3}x(t)\] となります。向きも考慮すると小球の運動方程式は
\[ m\frac{d^2 x}{dt^2}=-\frac{GMm}{R^3}x\]
であり,これより小球は周期 \(\displaystyle T=2 \pi \sqrt{\frac{R^3}{GM}}\) の単振動をすることがわかります。
小球の運動の様子
運動方程式から小球は周期 \(\displaystyle T=2 \pi \sqrt{\frac{R^3}{GM}}\) の単振動をすることがわかったのでこれを元に様々な運動の様子を調べてみましょう。
時刻 \(t\) における小球の位置 \(x(t)\)
\(x(0)=R\) より,変位 \(x(t)\) は
\[ x(t)=R \cos \left(\sqrt{\frac{GM}{R^3}} t \right)\]
となります。
時刻 \(t\) における小球の速度 \(v(t)\)
時刻 \(t\) における速度 \(v(t)\) は位置を微分して
\[ v(t)=\frac{dx}{dt}=-\sqrt{\frac{GM}{R}} \sin \left(\sqrt{\frac{GM}{R^3}} t \right)\]
と計算することが出来ます。
例題
地球トンネル問題ではでは上記のこと以外にも次のような問題を考えることが出来ます。ここでは以下の例題を見てみましょう。

【系の設定】のもとで以下の問に答えなさい。
(1) 小球が中心 O を通過するときの速度 \(v_0\) を次の2通りの方法で求めなさい。
① 単振動の力学的エネルギー保存則を使う方法
② 上で求めた \(x(t)\) から直接求める方法
(2) 実際に地球内部にトンネルを作り,小球を落とした場合,地球の裏側に到達するにはどの程度時間が必要か計算しなさい。ただし計算にあたっては
- 万有引力定数の大きさは 6.7 × 10-11 m3 kg-1 s-2
- 地球の質量は 6.0×1024 kg
- 地球の半径は 6.4×106 m
とすること。
(1) ① 単振動の力学的エネルギー保存則を使うと \[ \frac{1}{2}\frac{GMm}{R^3}R^2 =\frac{1}{2}mv_0^2\] これを \(v_0\) について解くと \[ v_0= \sqrt{\frac{GM}{R}}\]
(1) ② 時刻 \(t\) における速度 \(v(t)\) は \[ v(t)=\frac{dx}{dt}=-\sqrt{\frac{GM}{R}} \sin \left(\sqrt{\frac{GM}{R^3}} t \right)\] 小球が点Oに達する時刻は \(\displaystyle t=\frac{T}{4}=\frac{\pi}{2} \sqrt{\frac{R^3}{GM}} \) であるので,求める速度は \[\begin{align} v \left(\frac{T}{4} \right) &=-\sqrt{\frac{GM}{R}} \sin \left(\sqrt{\frac{GM}{R^3}} \frac{\pi}{2} \sqrt{\frac{R^3}{GM}} \right) \\ &= -\sqrt{\frac{GM}{R}} \end{align}\] これは①の結果と一致する。
(2) トンネルの入口から出口までかかる所要時間は周期の1/2なので \[ \frac{T}{2}=\pi \sqrt{\frac{R^3}{GM}} \simeq 2.5 \times 10^3 \text{s}\]
 あんとら
あんとら2500 秒 ≒ 42 分程度で地球の裏側までいけてしまうことがわかります



コメント