p-V グラフから熱効率を求める方法を例題を通してわかりやすく紹介します。
例題
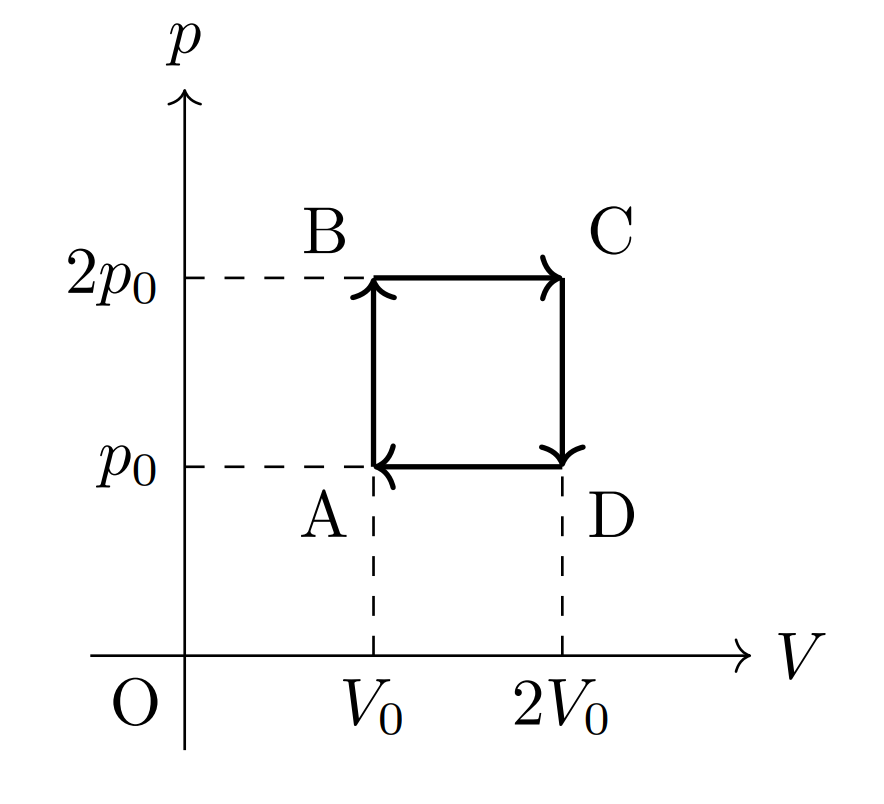
単原子分子からなる理想気体 \(n\) mol を容器に入れ，圧力 \(P\) と体積 \(V\) を A→B→C→D→A のように変化させた。この系の熱効率を求めたい。以下，A の絶対温度を \(T_0\) とし，気体定数を \(R\) とする。
(1) B，C，D の温度を \(T_0\) を用いて表しなさい。
(2) 各過程で気体のする仕事を求め，それらの総和 \(W_{total}\) を求めよ。
(3) 各過程の内部エネルギー変化 \(\Delta U\) を求めよ。
(4) 各過程で気体が熱源から得る熱量を符号も含めて示せ。
(5) この系の熱効率 \(e\) を求めよ。
p-V グラフから熱効率を求める問題は熱力学における応用問題として定期試験や大学入試でしばしば出題されます。
計算が多く，難しいですがこのようなタイプの p-V グラフの熱効率は次の流れにそって解くことが出来ます。
各点における温度を求める
各点における温度はボイル・シャルルの法則 \[\frac{pV}{T}=\text{const}\] を用いることによって求めることが出来ます。
この式を使うときには求めたい状態ともう１つ，既知の状態を知っている必要がありますが，ここではAの情報（\(p_0,V_0,T_0\)）を使えば良いですね。
B，C，Dの温度をそれぞれ \(T_B,T_C,T_D\) とするとボイル・シャルルの法則より \[\frac{p_0 V_0}{T_0}=\frac{2p_0 V_0}{T_B}\] \[\frac{p_0 V_0}{T_0}=\frac{2p_0 \cdot 2V_0}{T_C}\] \[\frac{p_0 V_0}{T_0}=\frac{p_0 \cdot 2V_0}{T_D}\] これより \[T_B=2T_0,\;T_C=4T_0,\;T_D=2T_0\]
系のする正味の仕事を求める
各点の温度が求まったので次にこの系（ A→B→C→D→A）がする正味の仕事を求めてみましょう。
系内部の圧力を \(p\)，微小な体積変化を \(\Delta V\) とすると気体のする仕事は \[\Delta W=p \Delta V\] で与えられる
これより，各過程でなす仕事を一つ一つ求めることが出来ます。
【A→B】
気体は定積変化をしているので \(\Delta V=0\) 。従って \[W_{AB}=0\]
【B→C】
\(p=2p_0\)，\(\Delta V=V_0\) より \[W_{BC}=2p_0 V_0\]
【C→D】
気体は定積変化をしているので \(\Delta V=0\) 。従って \[W_{CD}=0\]
【D→A】
\(p=2p_0\)，\(\Delta V=-V_0\) より \[W_{DA}=-p_0 V_0\]
以上より，正味の仕事 \(W_{total}\) は \[W_{total}=2p_0 V_0-p_0 V_0=p_0 V_0\]
ちょっと余談
(2) の結果から，p-V グラフで囲まれた部分の面積は気体のする仕事を表していることがわかります。
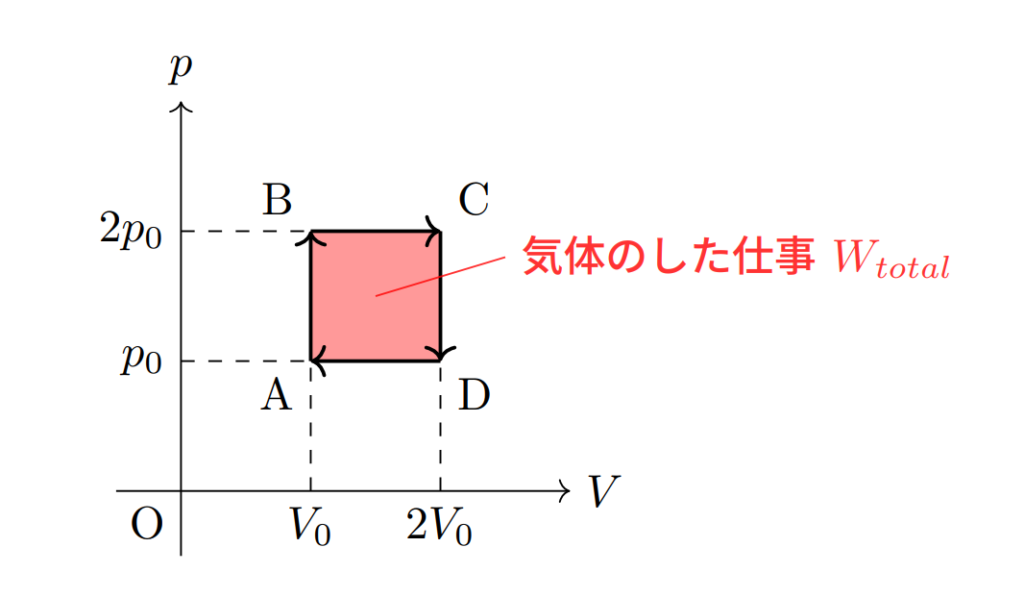
この事実は一般化することが可能で，次のように書くことが出来ます。
系内部の圧力を \(p\) 変化前後の体積を \(V_1,V_2\) とすると気体のする仕事 \(W\) は \[W=\int_{V_1}^{V_2}pdV\] で与えられる
内部エネルギー変化を求める
気体の内部エネルギー変化を求めます。気体の内部エネルギーは
まず，各点における内部エネルギーを求める。(1) より \[T_B=2T_0,\;T_C=4T_0,\;T_D=2T_0\] であることを用いると A，B，C，D の内部エネルギーは \[U_A=\frac{3}{2}nRT_0,\quad U_B=3nRT_0 \\U_C=6nRT_0,\quad U_D=3nRT_0\] これより各過程の内部エネルギー変化は気体の状態の方程式 \(p_0 V_0 =nRT_0\) も使って \[\begin{align}\Delta U_{AB}=\frac{3}{2}p_0 V_0 &\quad \Delta U_{BC}=3p_0 V_0 \\ \Delta U_{AB}=-3p_0 V_0 &\quad \Delta U_{AB}=\frac{3}{2}p_0 V_0 \end{align}\] である。
気体が得た熱量を求める
内部エネルギーの変化が求まったので，熱力学第１法則を使って気体が得た熱量を求めます。
気体が得た熱量を \(\Delta Q\)，気体がした仕事を \(W\)，気体の内部エネルギー変化を \(\Delta U\) とすると熱力学第１法則 \[\Delta Q=W+\Delta U\] が成り立つ
例えば，\(-Q\;(Q>0)\) の熱量を得た，ということは \(Q\) の熱量を放出した。という表現に置き換わることに注意しましょう。
【A→B】
\( W_{AB}=0\)，\(\displaystyle \Delta U_{AB}=\frac{3}{2}p_0 V_0\) より，気体が得た熱量は \[Q_{AB}=+\frac{3}{2}p_0 V_0\]
【B→C】
\( W_{BC}=2p_0 V_0\)，\(\displaystyle \Delta U_{BC}=3p_0 V_0\) より，気体が得た熱量は \[Q_{BC}=+5p_0 V_0\]
【C→D】
\( W_{CD}=0\)，\(\displaystyle \Delta U_{CD}=-3p_0 V_0\) より，気体が得た熱量は \[Q_{CD}=\color{red}{-}3p_0 V_0\]
【D→A】
\( W_{DA}=p_0 V_0\)，\(\displaystyle \Delta U_{DA}=-\frac{3}{2}p_0 V_0\) より，気体が得た熱量は \[Q_{DA}=\color{red}{-}\frac{1}{2}p_0 V_0\]
あんとら定積モル比熱の式を使うと内部エネルギーの変化を求めずに熱量を出すことも出来ますが，ここではややこしくなるので割愛しました
熱効率を求める
様々な情報を得ることが出来たので熱効率を求めます。
熱効率 \(e\) は \[e=\frac{\mathsf{気体がした正味の仕事}\; W_{total}}{\mathsf{気体が得た熱量}\; Q_{in}}\] で与えられる
ここで熱効率の分母における \(Q_{in}\) は「気体が得た正の熱量」であって系が得た正味の熱量 \(Q_{total}\) ではないことに注意しましょう。ここで系が得た熱量は \(Q>0\) の部分の和，すなわち \[\begin{align} Q_{in} &= Q_{AB}+Q_{BC}\\ &=5p_0 V_0+\frac{3}{2}p_0 V_0\\ &=\frac{13}{2}p_0 V_0 \end{align}\] と計算することが出来ます。
気体がした正味の仕事 \(W_{total}=p_0 V_0\)，気体が得た正味の熱量 \(\displaystyle Q=\frac{13}{2}p_0 V_0\) より，この熱機関の熱効率 \(e\) は \[e=\frac{W_{total}}{Q}=\frac{2}{13}\]
コメント