カルノーサイクルとカルノーサイクルに出てくる物理量(仕事,熱量,熱効率)を紹介します。
- カルノーサイクルとは何なのか
- カルノーサイクルの各過程における熱の出入りの計算方法
- カルノーサイクルの熱効率
カルノーサイクルとは
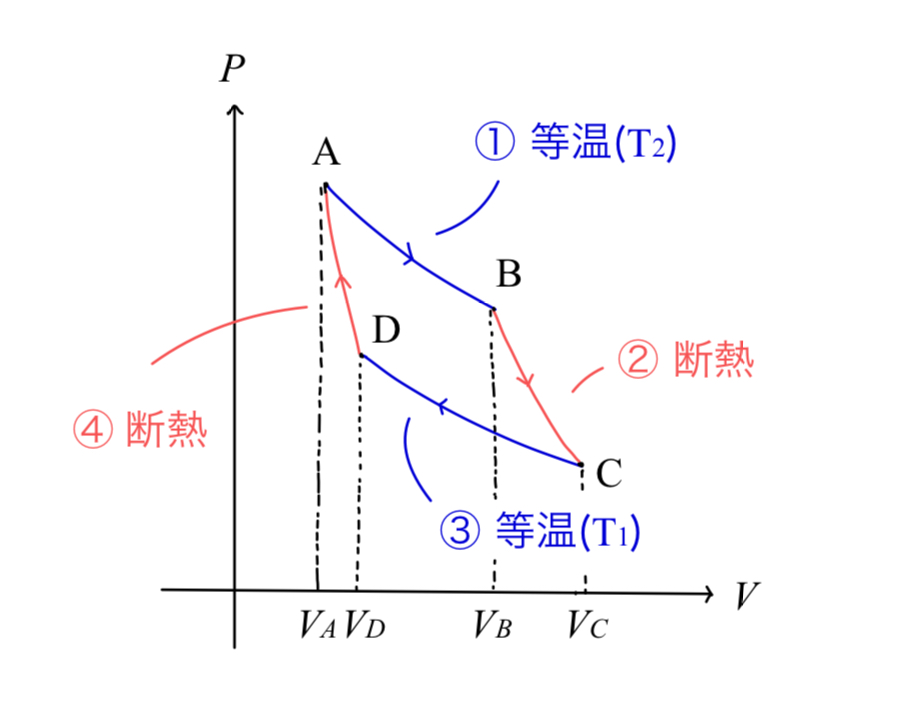
カルノーサイクルとは理想的な熱機関の基本原理を示すためのモデルで
- 等温膨張
- 断熱膨張
- 等温圧縮
- 断熱圧縮
の4つの過程からなります。
 あんとら
あんとら大学の熱力学の期末試験や大学入試物理の題材として使われることも多いです
系の設定
ここでは,次のように系を設定します。
- 図においてA → B → C → D のように系を変化させる
A→B:等温膨張,B→C:断熱膨張
C→D:等温圧縮,D→A:断熱圧縮 - 系の気体は理想気体である(すなわち常に \(pV=nRT\) が成り立つ)
- A→B間の温度は \(T_2\),C→D間の温度は \(T_1\) (\(T_1<T_2\))
- 定積モル比熱は \(C_V\)
ここでは各過程における熱の出入りを計算し,カルノーサイクルの熱機関について理解を深めます。
課程①:等温膨張の計算
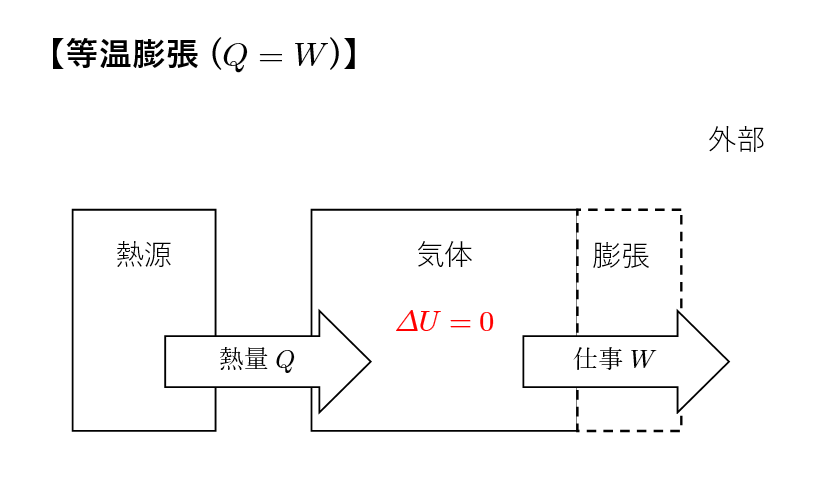

気体を等温的に膨張させます。この課程では気体が熱源と等温的にやり取りしながら膨張します。
等温課程なので気体の内部エネルギーは変化しません。
すなわち,課程①では常に \(\Delta U =0\) が成り立ちます。
このとき,熱力学第1法則 \(\Delta U = \Delta Q +W\) より,\(W=- \Delta Q\) となり,等温膨張では気体がした仕事分,外部の熱源から同じ大きさの熱を得ていることがわかります。



仕事分の熱量を外部から得られなかったらエネルギーが減ってしまいます
等温膨張で気体がする仕事
等温膨張で系がする仕事を求めてみましょう。
気体のする仕事は \(pdV\) を各体積で積分したもので算出されます。
気体のする仕事は \[W_{AB}=\int pdV\] で計算できる
ここで,今回は理想気体であるので気体の状態方程式 \(pV=nRT\) が常に成り立つことを用いると \[ \begin{align} W_{AB} &= \int p dV = \int_{V_A}^{V_B} \frac{nRT_2}{V} dV \\ &= nRT_2 \left[ \log |V| \right]_{V_A}^{V_B}\\ &= nRT_2 \log \frac{V_B}{V_A} \end{align}\] と計算出来ます。
等温膨張で外部から得る熱量
課程①では熱源から与えられる熱量 \(Q_{1}\) と気体のする仕事 \(W_{AB}\) は等しいので\[Q_{1}=W_{AB}=nRT_2 \log \frac{V_B}{V_A}\] と計算出来ました。
- 等温膨張では,気体の内部エネルギーが変化せず,系のする仕事と,系の奪われる熱量が等しい
- 系のする仕事 \(W_{AB}\) は \[W_{AB}= nRT_2 \log \frac{V_B}{V_A} \]
- 系が外部から得る熱量 \(Q_1\) も等しく\[Q_{AB}= nRT_2 \log \frac{V_B}{V_A} \]
課程②:断熱膨張
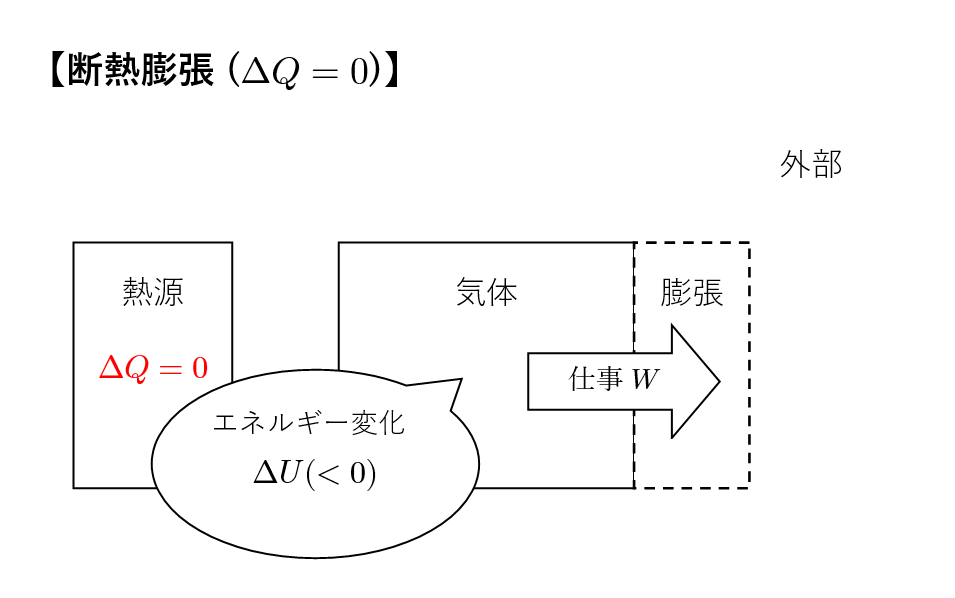

理想的な気体を断熱的に膨張させます。
この課程では外部との熱のやり取りがなく,\(\Delta Q=0\) が条件として成り立ちます。
これを熱力学第一法則に代入すると,\(\Delta U =W\) となり,内部エネルギーの変化量と気体がした仕事が等しいことがわかります。
断熱膨張における内部エネルギー変化
断熱過程では仕事を求めるのが難しいので,先に内部エネルギーの変化量を考えます。



圧力,体積が常に一定ではなく,積分変数を \(P,V\) で取ることが難しいです
温度が \(\Delta T\) 変化したときの内部エネルギー変化 \(\Delta U\) は \[\Delta U =n C_V \Delta T\] で与えられる
これより,内部エネルギーの変化量は\[ \Delta U= nC_V \Delta T =nC_V (T_1-T_2) \; (<0)\] と求まります。
断熱膨張で系のする仕事
断熱膨張では内部エネルギーの変化量と気体がした仕事が等しいので,気体のした仕事は \[ W_{BC}=nC_V (T_2-T_1) \; (>0)\] と求まります。
- 断熱膨張では熱の出入りがなく \(\Delta Q =0\)
- 内部エネルギーの変化は \(\Delta U =nC_V (T_1-T_2)\)
- 系のする仕事は \(W_{BC}=nC_V(T_2-T_1)\)
課程③:等温圧縮
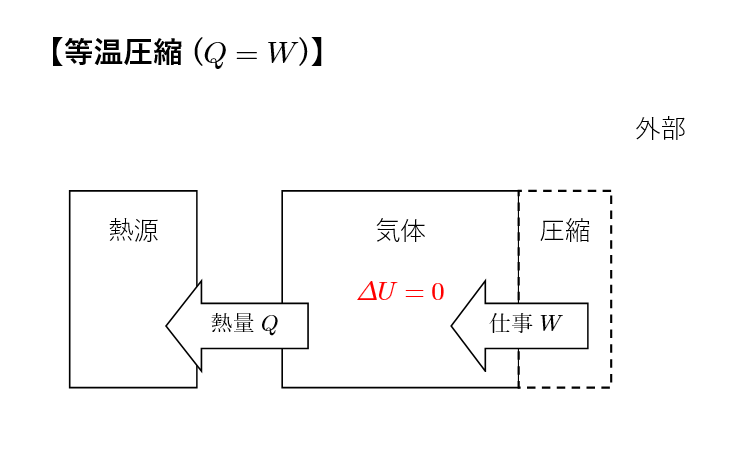

気体を等温的に圧縮します。この課程では気体が熱源から熱を受け取りながら圧縮されます。
ここでも課程①と同様,気体の内部エネルギーは変化せず \(\Delta U =0\) が成り立ちます。
等温圧縮で気体がされる仕事
等温圧縮で気体がされる仕事を求めてみましょう。
気体のする仕事は \[W_{AB}=\int pdV\] で計算できる
積分経路が C → D であることに注意して計算すると \[\begin{align} W_{CD} &=\int p dV = \int_{V_C}^{V_D} \frac{nRT_1}{V}dV \\ &= nRT_1 \left[ \log |V| \right]_{V_C}^{V_D}\\ &= nRT_1 \log \frac{V_D}{V_C} \\ &=-nRT_1 \log \frac{V_C}{V_D}\end{align}\]となります。
\(V_C > V_D\) より,\(\log (V_C /V_D)>0\) であり,これより \( W_{CD} <0\) がわかります。
\(W_{CD}\) は気体のする仕事で定義しているので,\( W_{CD} <0\) より気体は外部から仕事をされていることがわかります。
等温圧縮で系が外部に放出する熱量
等温圧縮で系が外部に放出する熱量を求めます。
過程①と同様,内部エネルギー変化は0なので放出した熱量はそれぞれ\[Q_2=-nRT_1 \log \frac{V_C}{V_D}\] となり,言い換えると,等温圧縮では系は \[|Q_2|=nRT_1 \log \frac{V_C}{V_D}\] の熱量を吸収していることがわかります。
- 等温過程なので \(\Delta U =0\)
- 気体は外部から仕事をされ,その大きさは \[|Q_2|= nRT_1 \log \frac{V_C}{V_D}\]
- 気体は外部に熱量を放出し,その大きさは\[|Q_2|= nRT_1 \log \frac{V_C}{V_D}\]
課程④:断熱圧縮
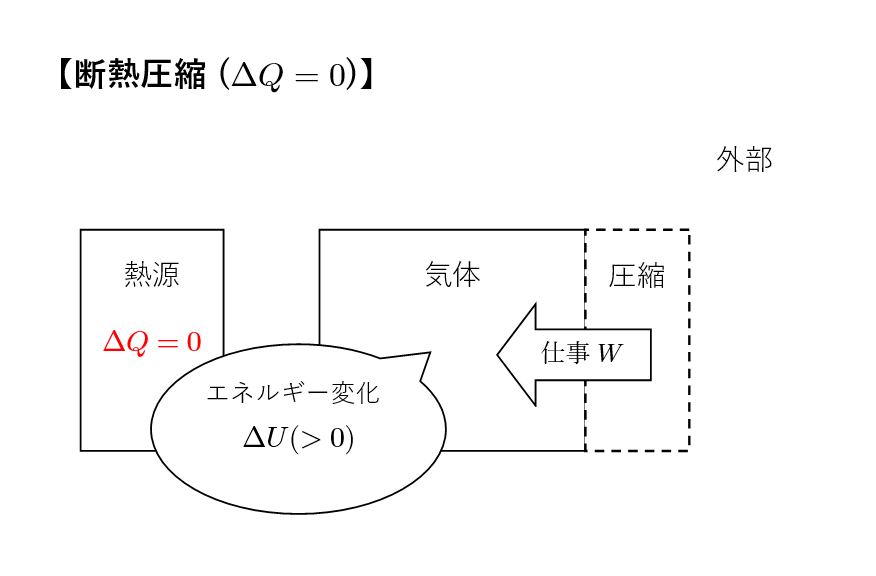

気体が断熱的に圧縮されます。再び、外部との熱のやり取りはありませんが、気体の内部エネルギーが仕事に変換されます。
ここでも課程②と同様,外部との熱のやり取りがないので,\(\Delta Q=0\) が条件として成り立ちます。
系の内部エネルギー変化
温度変化が \(\Delta T =T_2 – T_1 \) であることを考えると \[ \Delta U=nC_V (T_2-T_1)\] となります。
\(\Delta U>0\) より気体の内部エネルギーは増加していることがわかります。
系のする仕事
断熱膨張のときと同じように考えると \[W_{DA}=-\Delta U =nC_V (T_1-T_2)\] と計算することが出来ます。
ここで \(W_{DA}<0\) より,気体は外部から仕事をされていることがわかります。
- 断熱過程なので熱の出入りがなく \(\Delta Q =0\)
- 気体の内部エネルギーは増加し,その大きさは \( \Delta U=nC_V (T_2-T_1)\)
- 気体は外部から仕事をされ,その大きさは \(W_{DA}=nC_V (T_2-T_1)\)
カルノーサイクルの体積比に関する性質
カルノーサイクルの性質として\[\frac{V_B}{V_A}=\frac{V_C}{V_D}\]が成り立ちます。



この体積比の関係式は特に等温状態の気体の仕事を考える際に重要です
導出の際には,断熱課程②,④においてポアソンの式
\[TV^{\gamma -1}=\text{const}\]を用います。
課程②と課程④は断熱課程であるので,ポアソンの式\[TV^{\gamma -1}=\text{const}\]が成り立つ。
課程②において\[T_2 V_B^{\gamma -1}=T_1 V_C^{\gamma -1}\]課程④において\[T_2 V_B^{\gamma -1}=T_1 V_C^{\gamma -1}\]よって,これらから \(T\) を消去すると\[\frac{V_B}{V_A}=\frac{V_C}{V_D}\]となり,求める式を得る。
カルノーサイクルの熱効率の計算
カルノーサイクルの熱効率を計算します。
サイクルの全体のなす仕事
サイクル全体での仕事を \(W_{sum}\) とすると \[\begin{align} W_{sum} &= W_{AB}+W_{BC}+W_{CD}+W_{DA} \\ &=nRT_2 \log \frac{V_B}{V_A} -nRT_1 \log \frac{V_C}{V_D} \\ &=nR(T_2-T_1)\log \frac{V_B}{V_A} \end{align}\] ここで,最後の式変形では
A,B,C,D の体積の \(V_A,V_B,V_C,V_D\) について \[\frac{V_B}{V_A}=\frac{V_C}{V_D}\]が成り立つ
ことを用いました。
サイクル全体の熱量変化
過程②,④(断熱変化)では熱量の変化はなく,過程①,③(等温変化)では,前述の通り仕事と熱量の値は等しいので熱量は仕事と同じく \[Q=nR(T_2-T_1)\log \frac{V_B}{V_A}\] と計算できます。
カルノーサイクルの熱効率
熱効率とは,熱機関の得た熱量に対する熱機関のした正味の仕事の割合のことです。
\(Q_1\) を外部に放出した熱量,\(Q_2\) を外部から吸収した熱量とすると,カルノーサイクルの熱効率 \(\eta\) は \[\eta=1-\frac{Q_1}{Q_2}=1-\frac{T_1}{T_2}\] で与えられる
熱効率を実際に導出してみましょう。
\(Q\) の表式の導出
ここで,サイクルを一周した際の内部エネルギーの変化はゼロであるので \(\Delta U=0\)(内部エネルギーは温度に依存する状態量であるので,\(\Delta U =U_A-U_A=0\) となります。
また,サイクルを一周した際の熱機関の吸収した正味の熱量 \(Q\) は \[Q=Q_2-Q_1\] であるので,熱力学第一法則から \[W=Q_2-Q_1\] となります。
よって \[\begin{align} \eta &=\frac{W}{Q_2} \\ &=\frac{Q_2-Q_1}{Q_2}=1-\frac{Q_1}{Q_2}\end{align}\] となり,熱効率を求めることができます。
\(T\) の表式の導出
前述の各過程の熱量の計算より \[Q_1=nRT_1 \log \frac{V_B}{V_A}\] \[Q_2=nRT_2 \log \frac{V_B}{V_A}\] これより,\(Q_1/Q_2\) の値を計算すると\[\frac{Q_1}{Q_2} =\frac{T_1}{T_2}\] であるので \[\eta =1-\frac{T_1}{T_2}\] となり,求まります。

コメント