クーロンの法則と静電場の関係を微積分やベクトルを使ってわかりやすく解説します。
クーロンの法則
電磁気学の根幹となるクーロンの法則は次の式で与えられます。
2つの点電荷 \(q,q_1\) が \(\boldsymbol{r}_0,\boldsymbol{r}_1\) にあるとき \(q_1\) から \(q\) にはたらく力は \[ \boldsymbol{F}=kqq_1 \frac{ \boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|^3}\]
この法則はクーロンの実験によって発見されたもので,簡潔に
2つの点電荷の間には,各々の点電荷の積に比例し,点電荷間の距離の2乗に反比例した大きさの力が電荷間の直線方向に働く
ということを表します(上の式では1つの点電荷にかかる力のみに言及しています)。
また,\(k\) はクーロンの比例定数で,電荷 \(\text{C}\) を用いるSI単位系ではおよそ \[ k=8.99 \times 10^9 \; \text{N m}^2/ \text{C}^2\] であることが実験的に知られています。真空の誘電率を \(\varepsilon_0\) とし,\(\displaystyle k= \frac{1}{4 \pi \varepsilon_0}\) とおくと \[ \boldsymbol{F}=\frac{qq_1}{4 \pi \varepsilon_0} \frac{ \boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|^3}\] と書くことも出来ます。
ベクトル表記の意味
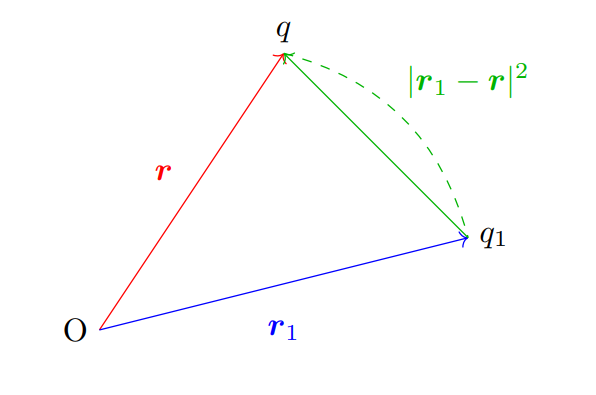
\[ \boldsymbol{F}=\frac{qq_1}{4 \pi \varepsilon_0} \frac{ \boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|^3}\] は高校で習うクーロンの法則とは少し形が違いますが,\[\boldsymbol{F}=\frac{qq_1}{4 \pi \varepsilon_0 |\boldsymbol{r}_0-\boldsymbol{r}_1|^2}\color{red}{\frac{\boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|}} \] と書き直し
- \(\displaystyle \color{red}{\frac{\boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|}}\) の部分は \(q_1\) から \(q\) に向かう単位ベクトルである
- \(|\boldsymbol{r}_0-\boldsymbol{r}_1|^2\) はベクトルの絶対値→2つの点電荷間の距離
と考えると高校物理で習うクーロンの法則 \[F=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\] とは少し表記が違うものの,示す内容は同じであることがわかります。
 あんとら
あんとら以下では,1つの電荷 \(q\) を固定し,\(q\) にはたらく力について考えます
クーロンの法則の重ね合わせ
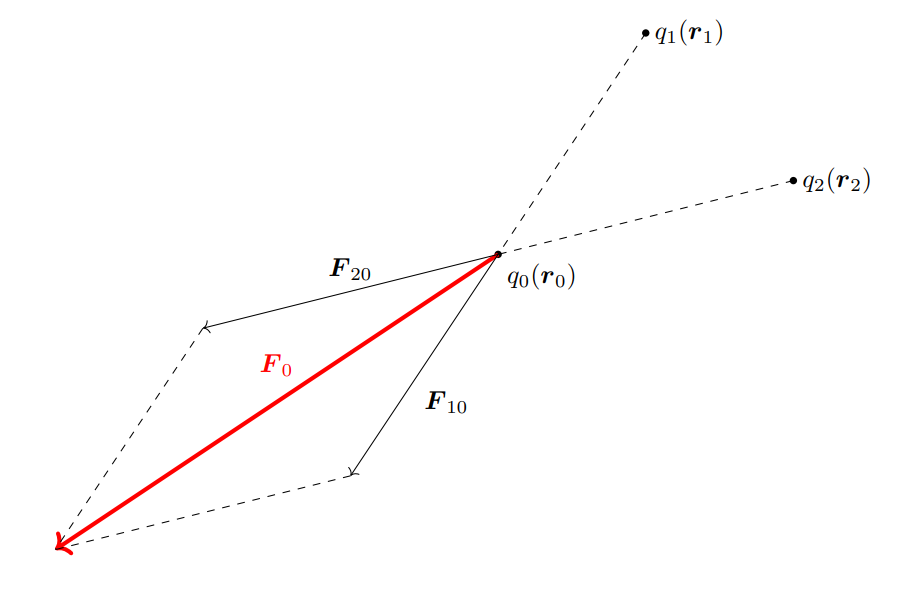

クーロンの法則は電荷が3つ以上のときにも成り立ちます。例えば3個の点電荷 \(q_0\),\(q_1\),\(q_2\) があるとき,\(q\) にはたらく力は上の図のようになり \[\boldsymbol{F}_0=\boldsymbol{F}_{10}+\boldsymbol{F}_{20}\] と書けます。
これを重ね合わせの原理といいます。この重ね合わせの原理は一般に拡張することが可能で,次のように書くことが出来ます。
電荷が \(n+1\) 個あるとき,点電荷 \(q_0\),\(q_1\),\(q_2\),\( \cdots\),\( q_n\) の位置ベクトルを \(\boldsymbol{r}_0\),\(\boldsymbol{r}_1\),\(\boldsymbol{r}_2\),\(\cdots\), \(\boldsymbol{r}_n\) とすると電荷 \(q\) にはたらく力は \[\boldsymbol{F}=\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^{n}\frac{q_0 q_i (\boldsymbol{r}_0-\boldsymbol{r}_i)}{|\boldsymbol{r}_0-\boldsymbol{r}_i|^3}\]
静電場の式とクーロンの法則
ファラデーは,電荷 \(q\) が力を受けているとき,この力 \(\boldsymbol{F}\) が単位電荷に働く電気的な場によって与えられる,すなわち \[\boldsymbol{E}(\boldsymbol{r})=\frac{\boldsymbol{F}}{q}\] で定義される \(\boldsymbol{E}(\boldsymbol{r})\) を用いて \[\boldsymbol{F}=q\boldsymbol{E}(\boldsymbol{r})\] と表すことが出来ると考えました。この \(\boldsymbol{E}(\boldsymbol{r})\) のことを電場といいます。
点電荷が作る電場
点電荷から受ける力は \[ \boldsymbol{F}=\frac{q_0 q_1}{4 \pi \varepsilon_0} \frac{ \boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|^3}\] と書くことが出来たので \[\boldsymbol{E}(\boldsymbol{r}) =\frac{q_1}{4 \pi \varepsilon_0} \frac{ \boldsymbol{r}_0-\boldsymbol{r}_1}{|\boldsymbol{r}_0-\boldsymbol{r}_1|^3}\] とすると,この \(\boldsymbol{E}(\boldsymbol{r})\) は点電荷 \(q_1\) が作る電場(=この電場によって \(q_0\) は \(q_0 \boldsymbol{E}(\boldsymbol{r})\) の力を受ける)と解釈することが可能になります。
電場の重ね合わせの原理
電場についてもクーロン力と同様に重ね合わせの原理 \[\boldsymbol{E}(\boldsymbol{r})=\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^{n}\frac{ q_i (\boldsymbol{r}_0-\boldsymbol{r}_i)}{|\boldsymbol{r}_0-\boldsymbol{r}_i|^3}\] が成り立ちます。
連続分布する電荷の作る電場
これまでは電場の重ね合わせは \(n\) 個の電荷の重ね合わせとして離散的に見てきましたが,この式を連続的に考えます。
連続的に考えるためにここでは次の図のような系を設定します。
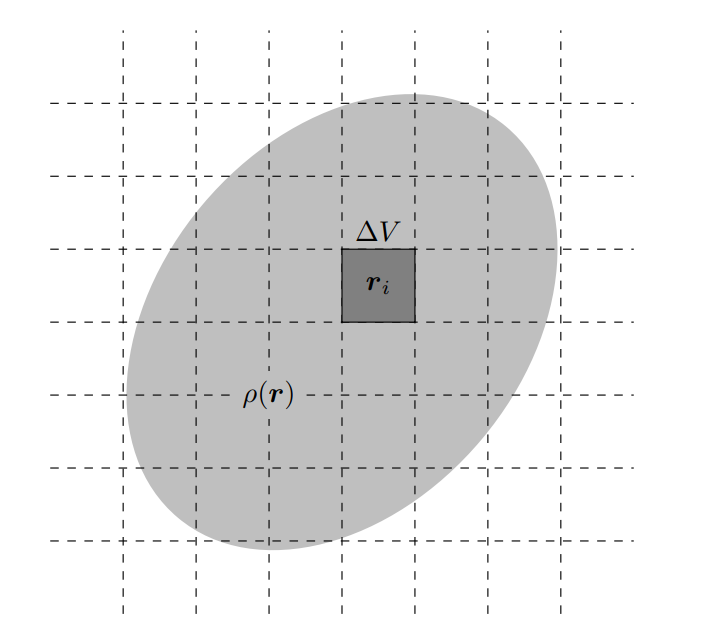

- 電荷が空間のある領域にわたって密度 \(\rho (\boldsymbol{r})\) で分布している
- 領域を \(n\) 個の微小体積に分割し,その要素を \(\Delta V\) とする
- 微小な体積要素の位置ベクトルを \(\boldsymbol{r}_i \) \( (i=1,2,\cdots n)\) とする
このとき,電荷が \(\boldsymbol{r}\) につくる電場は \[\frac{\rho (\boldsymbol{r_i}) \Delta V}{4 \pi \varepsilon_0} \frac{\boldsymbol{r}_0-\boldsymbol{r}_i}{|\boldsymbol{r}_0-\boldsymbol{r}_i|^3}\] で与えられるので \(i\) について和をとると重ね合わせの原理から \[\boldsymbol{E}(\boldsymbol{r})=\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^{n}\frac{\boldsymbol{r}_0-\boldsymbol{r}_i}{|\boldsymbol{r}_0-\boldsymbol{r}_i|^3} \rho (\boldsymbol{r_i}) \Delta V\] \(\Delta V \to 0 \ (n \to \infty)\) とすると \[\boldsymbol{E}(\boldsymbol{r})=\frac{1}{4 \pi \varepsilon_0} \int \frac{\boldsymbol{r}_0-\boldsymbol{r}’}{|\boldsymbol{r}_0-\boldsymbol{r}’|^3} \rho (\boldsymbol{r’})dV’\] となり,積分形の電場の式を得ることができます。



実際の計算では,適当な座標系を設定する必要があり,計算は煩雑になりがちです
直交座標では \(\boldsymbol{r}’=(x’,y’,z’)\) とすれば \(dV’=dxdydz\) と書けるので積分形の電場の式は \[E_x(x’,y’,z’)=\frac{1}{4 \pi \varepsilon_0} \iiint \frac{(x-x’)\rho (x’,y’,z’)}{[(x-x’)^2+(y-y’)^2+(z-z’)^2]^{\frac{3}{2}}} dxdydz \]と書くことが出来ます(\(y,z\) 成分も同様に書き下せます)。実際には
- 表記が非常に煩雑
- \(\rho (x’,y’,z’)\) が全座標においてわかるケースは稀(試験問題等では一定とする場合が多い)
ので,一般的な議論をする際は \(\boldsymbol{r}\) でまとめます。
例題
電場の重ね合わせを例題を通して実際に求めてみましょう。
半径 \(a\) の円状の導線を考える。中心を通る軸を取り,円の中心をOとする。線密度 \(\lambda\) で電荷が一様に分布しているとき,中心Oから距離 \(r\) にある点Pに生じる電場 \(E(r)\) を求めよ。
積分形の電場を求める際はまず微小部分の電場の成分を求めます。
積分といえどやることは「1つ1つの要素を足し合わせる」にすぎないので,頑張って計算してみましょう。
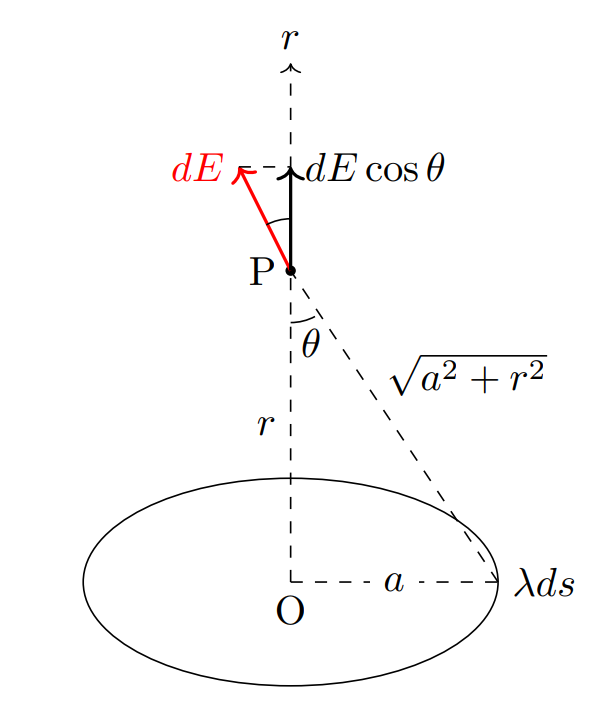

導線上の微小線分を \(ds\) とする。このとき,微小線分上には \( \lambda ds\) の電荷が分布するので,点Pに生じる電場の成分は \[dE=\frac{1}{4 \pi \varepsilon_0} \frac{\lambda ds}{a^2+r^2}\] 対称性より,軸に垂直な成分は打ち消されるので軸に平行な要素を考えれば良い。図のように \(\theta\) を取ると \(\displaystyle \cos \theta =\frac{r}{\sqrt{a^2+r^2}}\) であるので \[dE(r)=dE \cos \theta =\frac{1}{4 \pi \varepsilon_0} \frac{r \lambda ds}{(a^2+r^2)^{\frac{3}{2}}}\] これを円を経路として積分すると \[\begin{align} E(r) &= \oint \frac{1}{4 \pi \varepsilon_0} \frac{r \lambda }{(a^2+r^2)^{\frac{3}{2}}}ds \\ &= \frac{1}{4 \pi \varepsilon_0} \frac{r \lambda }{(a^2+r^2)^{\frac{3}{2}}} \oint ds \\ &= \frac{ar \lambda}{2 \varepsilon_0 (a^2+r^2)^{\frac{3}{2}}} \end{align}\]



ここで \(\displaystyle \oint ds\) は円周の長さ \(2 \pi a\) になることを使いました


コメント