マクローリン展開,およびマクローリン展開を用いてオイラーの公式 \[e^{i\theta} = \cos \theta +i \sin \theta\] について,高校数学でもわかる証明を紹介します。
- マクローリン展開とテイラー展開の基本原理
- 様々な関数を展開の具体的な方法
テイラー展開とマクローリン展開
関数 \(f(x)\) が何回でも微分可能で
\[\begin{align} &f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n \\ &= f(a)+\frac{f^{(1)}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n +\cdots \end{align}\]
とできるとき,これを関数 \(f(x)\) の \(a\) 近傍でのテイラー展開といいます。また,テイラー展開において特に \(a=0\) とした
\[ \begin{align} &f(x) =\sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n \\ &=f(0)+\frac{f^{(1)}(0)}{1!}x+\frac{f^{(2)}(0)}{2!}x^2+ \cdots + \frac{f^{(n)}(0)}{n!}x^n +\cdots \end{align}\]
をマクローリン展開といいます。
 あんとら
あんとら見た目がいかつい
式だけ見ても何を意味しているのかよくわからないので,以下で簡単な原理を説明します。
関数を多項式で近似する考え
数学や物理では \(\sin x\) や \(\cos x\) ,\(\log x\) といった様々な関数が出てきますが,これらの関数を \(x\) のべき級数 \[\sum_{n=0}^{\infty} a_n x^n = a_0 + a_1 x +a_2 x^2 + \cdots + a_n x^n + \cdots\] で表せると便利な時が多々あります。



具体的な値を入れると値がすぐにわかるのは整式で表す1つのメリットです
そこでこれらの関数を \(x\) だけの整式 \[f(x)=a_0 + a_1 x + \cdots +a_n x^n+ \cdots\] の形で表したい,というのがテイラー展開の簡単な主張です。
例:\(\sin x\) の \(x=0\) 付近での多項式近似
例として \(y=f(x)= \sin x\) を \(x=0\) 近傍で多項式で表してみます。
唐突ですが,\(y=f(x)= \sin x\) (緑色のグラフ)と \(\sin x\) の \(x=0\) での接線 \(y=x\) (青色のグラフ)を同一平面上に図示すると以下の通りになります。
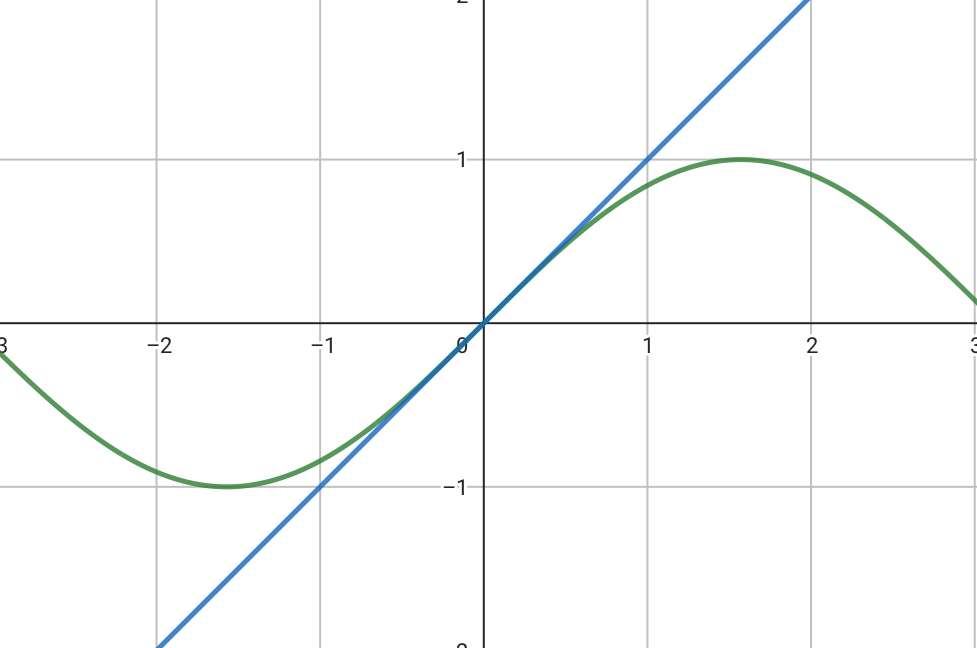

図から \(x\) が0から離れると2つのグラフは全く異なる挙動を示しますが \(x=0\) 付近を更に拡大すると
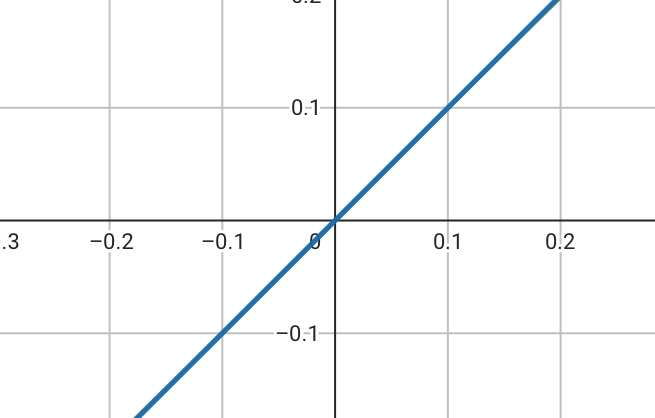

となり,\(y=\sin x\) と \(y=x\) は \(x=0\) 付近では殆ど同じに見なせることがわかります。
このとき \(\sin x\) は \(y=x\) という1次の多項式で近似出来ており,これが曲線 \(y=\sin x\) の第1次近似になります。



接線は関数の1次近似であるといえます
関数の第1次近似
一般的に考えます。
曲線 \(y=f(x)\) に対して,\(x=a\) における接線の方程式は \[y=f'(a) (x-a)+f(a)\] であり,この式が1次近似そのものであったので \(x=a\) 近傍における曲線 \(y=f(x)\) の1次近似の式は \[f(x) \simeq f'(a) (x-a)+f(a)\] と書けます。
微分可能な曲線 \(y=f(x)\) は \(x=a\) 近傍で \[f(x) \simeq f'(a)(x-a)+f(a)\] と表せる
近似の精度を上げる
近似の精度を上げることを考えます。



微分を繰り返していけば近似の精度が上がりそう
いま,1次の近似式は \[f(x) \simeq f'(a) (x-a)+f(a)\] と書けたので,今度は2次の近似を
\[f(x) \simeq f(a)+ f'(a)(x-a)+ a_2 (x-a)^2\]
の形でおいてみます(\(a_2\) は未定の定数です)。
1次の近似を求めるときは1回微分をしたので,今度は両辺を2回微分してみます。すると \[f^{(2)}(x) = 2a_2\] より,\(x=a\) を代入し \[ a_2 = \frac{f^{(2)}(a)}{2} \] であることがわかります。
したがって,関数 \(f(x)\) の第2次近似は \(a_2\) を代入した \[ f(x) \simeq f(a) + f'(a)(x-a)+ \frac{f^{(2)}(a)}{2} (x-a)^2\] で表されることがわかります。
(2回以上)微分可能な曲線 \(y=f(x)\) は \(x=a\) 近傍で \[ f(x) \simeq f(a) + f'(a)(x-a)+ \frac{f^{2}(a)}{2} (x-a)^2 \] と表せる
同様にして3次,4次,…,\(n\) 次の近似の式を求めていくと
\[ f(x)=f(a)+\frac{f^{(1)}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n +\cdots \]
となります。このようにして \(f(x)\) をテイラー展開することが出来ます。
マクローリン展開
これまでテイラー展開について紹介してきましたが,テイラー展開の式 \[ f(x)=f(a)+\frac{f^{(1)}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n +\cdots \] において,特に \(a=0\) の場合のテイラー展開のことをマクローリン展開といいます。
\(f(x)\) が何回で微分可能であるとき
- \(f(x)\) の \(x=a\) 近傍でのテイラー展開は \[ f(x)=f(a)+\frac{f^{(1)}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n +\cdots \]
- マクローリン展開は \[ f(x) =f(0)+\frac{f^{(1)}(0)}{1!}x+\frac{f^{(2)}(0)}{2!}x^2+ \cdots + \frac{f^{(n)}(0)}{n!}x^n +\cdots \]



実用上マクローリン展開の方が便利( \((x-a)^n\) の二項展開をしなくて良い)なので様々なところで使われます
マクローリン展開の具体例
実際に色々な関数をマクローリン展開してみると次の通りになります。
- \(\sin x\) のマクローリン展開は \[ \sin x = x- \frac{1}{3!}x^3 +\frac{1}{5!}x^5 + \cdots + (-1)^n \frac{x^{2n+1}}{(2n+1)!}+\cdots \]
- \(\cos x\) のマクローリン展開は \[ \cos x = 1- \frac{1}{2!}x^2 +\frac{1}{4!}x^4 +\cdots + (-1)^n \frac{x^{2n}}{(2n)!} +\cdots\]
- \(e^x\) のマクローリン展開は \[ e^x = 1+x+ \frac{1}{2}x^2 +\frac{1}{3!}x^3 \cdots +\frac{1}{n!}x^n +\cdots \]
マクローリン展開を使ってオイラーの公式を導出する
マクローリン展開の応用として,有名な等式 \[e^{i \theta} = \cos \theta + i \sin \theta\] を導出することが出来ます。
上のマクローリン展開の具体例より \[\begin{align} &\sin x = x- \frac{1}{3!}x^3 +\frac{1}{5!}x^5 + \cdots + (-1)^n \frac{x^{2n+1}}{(2n+1)!}+\cdots \\ &\cos x = 1- \frac{1}{2!}x^2 +\frac{1}{4!}x^4 +\cdots + (-1)^n \frac{x^{2n}}{(2n)!} +\cdots\\ &e^x = 1+x+ \frac{1}{2}x^2 +\frac{1}{3!}x^3 + \cdots +\frac{1}{n!}x^n +\cdots \end{align}\] である。ここに \(x=i \theta\) (\(i\)は虚数,\(\theta\) は実数)を代入すると \[ \begin{align} e^{i \theta} &= 1+\frac{i \theta}{1!}+ \frac{(i \theta)^2}{2!} +\frac{(i \theta)^3}{3!}+\frac{(i \theta)^4}{4!}\cdots
\\ &= \left( 1- \frac{\theta^2}{2!} +\frac{\theta^4}{4!} +\cdots \right)+ i \left(x- \frac{\theta^3}{3!} +\frac{\theta^5}{5!} + \cdots \right)
\\&= \cos \theta +i \sin \theta \end{align}\] となり,オイラーの公式を導出できる。
ここで得たオイラーの公式 \(e^{i\theta} = \cos \theta +i \sin \theta\) に \(\theta = \pi \) を代入するとオイラーの等式 \[e^{i\pi} = -1\] を得ることが出来ます。

コメント